Классический метод рассчета переходных процессов.
Модели источников и единичная функции.
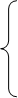 |
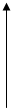 1(t)
1(t)
0, t<0

 1(t)=
1(t)=

 t 1, t>=0
t 1, t>=0
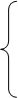




 tK=0
tK=0
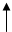

 0, t<0
0, t<0
e(t) U(t) U(t)=
 e(t), t>=0
e(t), t>=0
U(t)=e(t)*1(t)




 tK=0
tK=0



 0, t<0
0, t<0
Y(t) i(t)=
 Y(t), t>=0
Y(t), t>=0
i(t)=Y(t)*1(t)
ICX. Цепь первого порядка.











 r 1) расчет цепи до конца или расчет независимых
r 1) расчет цепи до конца или расчет независимых
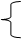

 E C начальных условий (ННУ): UC(0)
E C начальных условий (ННУ): UC(0)
 IL(0).
IL(0).
UC(0)=0 {UC(0_)=UC(0+)=UC(0)=0)
2) рассчёт: после коммутации
i(t)
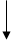








 E=UR+UC
E=UR+UC


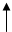

 R E=iR+UC
R E=iR+UC

 E C UC E=R*C*(dUC/dt)+UC)
E C UC E=R*C*(dUC/dt)+UC)


dUC/dt= -1/RC * UC+ 1/RC *E
 |  |  |  |  | |||||
X’ = A 1 * X + B 1* V
t –постоянная t-ии цепи t =R*C
dUC/dt + 1/ t *UC= 1/ t *E dUC/dt +1/ t *UC=0
&+1/ t =0 &=-1/ t =1/R*C
UC(t)=UНЧ+UОО=UС УСТ+ UС СВ UОО= UС СВ=A*(e)&t= A*(e)-t/ t
UС УСТ=UНЧ


 iC=C*(dUC/dt)=0 t
iC=C*(dUC/dt)=0 t
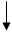



 (1/ t)* UС УСТ=(1/ t)*E
(1/ t)* UС УСТ=(1/ t)*E
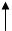

 UС УСТ=E UС УСТ=E
UС УСТ=E UС УСТ=E

UC(t)=UС УСТ+ UС СВ=E+A*(e)-t/ t
A-?

 t=0 UC(0)=E+A 0=A+E A=-E
t=0 UC(0)=E+A 0=A+E A=-E
UC(t)= E*(1-e-t/ t ) iC(t)=C*(dUC/dt)=E/R* e-t/ t
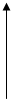 E(t)
E(t)
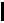
 E
E

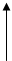 UC t =R*c – постоянная времени цепи.
UC t =R*c – постоянная времени цепи.
E
 |
-определяет t, за которое функция уменьшается в e раз.

i(t) Переходный процесс обычно заканчивается за 3-4 t.

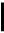


 E/R
E/R

r До коммутация: ННУ Uc(0-)=Uc(0+)=Uc(0)=E
C
 После коммутации: Uc+Ur=0 Ur=i*r
После коммутации: Uc+Ur=0 Ur=i*r 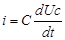
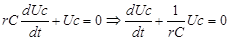

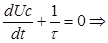 Характеристическое уравнение
Характеристическое уравнение
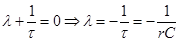 ; Uc(t)=Ucуст+Ucсв;
; Uc(t)=Ucуст+Ucсв; 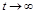 Uc уст=0
Uc уст=0
Uс св=
Uc(t)=Uc уст+Uc св 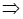 t=0 Uс(0)=Uс уст+A
t=0 Uс(0)=Uс уст+A 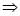 A=Uc(0)-Uc уст=E (Uc уст=
A=Uc(0)-Uc уст=E (Uc уст=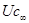 )
)
Ответ: Uc(t)=E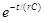 i c(t)=
i c(t)=
 2014-02-13
2014-02-13 421
421








