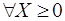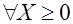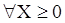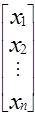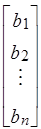Таблица 1.1
.
Пример 1.3 записать в форме КЗЛП следующую ОЗЛП: найти max целевой функции F = X1 + X2 - X3 при ограничениях
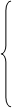 X1 + X2 + X3
X1 + X2 + X3  7,
7,
2X1 - X2 + X3 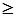 2,
2,
X1 - X2 + 5X3 = 8,
X1 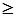 0.
0.
Решение. Сначала избавимся от отсутствия условий неотрицательности на переменные Х2 и Х3. Для этого сделаем замены:
|
Тогда исходная задача будет записана в следующей форме:
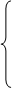 X1 + X2 + X3 - X4 - X5
X1 + X2 + X3 - X4 - X5  7,
7,
2X1 - X2 + X3 + X4 - X5 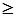 2,
2,
X1 - X2 + 5X3 + X4 - 5X5 = 8,
|
 и F = - X1 - X2 +X3 +X4 - X5 min.
и F = - X1 - X2 +X3 +X4 - X5 min.
Введя в систему еще две неотрицательные переменные X6 и X7, избавимся от неравенств и получим следующую КЗЛП:
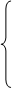 X1 + X2 + X3 - X4 - X5 + X6 = 7,
X1 + X2 + X3 - X4 - X5 + X6 = 7,
2X1 - X2 + X3 + X4 - X5 + X7 = 2,
X1 - X2 + 5X3 + X4 - 5X5 = 8,
|
 и F = - X1 - X2 +X3 +X4 - X5 min.
и F = - X1 - X2 +X3 +X4 - X5 min.
Использование матриц дает возможность записать ОЗЛП в компактной форме.
Введем:
1. Матрицу коэффициентов (условий)
A = 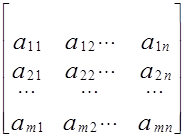
| |||
| |||
4. Вектор цели. C = 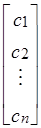
Тогда эту задачу можно записать в виде
AX 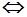 B, (1.9)
B, (1.9)
X 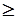 0, (1.10)
0, (1.10)
 F = CX extr. (1.11)
F = CX extr. (1.11)


 Здесь Сх означает скалярное произведение векторов С и Х (C·X=
Здесь Сх означает скалярное произведение векторов С и Х (C·X=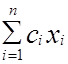 ); Ах - произведение матрицы А на вектор Х с компонентами
); Ах - произведение матрицы А на вектор Х с компонентами 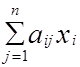 , i=1,m, которые согласно векторному равенству должны равняться соответствующим компонентам вектора В, т.е.
, i=1,m, которые согласно векторному равенству должны равняться соответствующим компонентам вектора В, т.е. 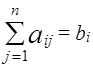 ; векторное неравенство Х
; векторное неравенство Х 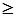 0 означает, что каждая компонента вектора Х должна быть неотрицательной.
0 означает, что каждая компонента вектора Х должна быть неотрицательной.
Теперь ОЗЛП может быть сформулирована так: найти неотрицательный вектор (1.10), удовлетворяющий ограничению (1.9), при котором целевая функция (1.11) обращается в экстремум.
1.1 Примеры применения методов линейного программирования
Пример1.4. Небольшая фабрика изготовляет два вида красок: для внутренних (В) и наружных работ (Н). Продукция обоих видов поступает в оптовую продажу. Для производства красок используются два исходных продукта - А и Б. Максимально возможные суточные запасы этих продуктов составляют 6 и 8 т соответственно. Расходы А и Б на 1 т соответствующих красок приведены в табл. 1.1.
| Исходный продукт | Расход исходных продуктов (т) на 1 т краски | Максимально возможный Запас (т) | |
| Краска Н | Краска В | ||
| А | |||
| Б |
Изучение рынка сбыта показало, что суточный спрос на краску В никогда не превышает спроса на краску Н более, чем на 1 т. Установлено, что спрос на краску Н никогда не превышает 2 т. в сутки.
Оптовая цена краски В - 3 тыс. руб.; краски В - 2 тыс. руб.
Требуется определить, какое количество краски каждого типа должна производить фабрика, чтобы доход от реализации продукции был максимальным.
Построение математической модели (ММ)
Процесс построения ММ для решения поставленной задачи нужно начать с ответов на вопросы:
1. Для определения каких величин должна быть построена ММ? Другими словами, как идентифицировать (идентификация – отождествление) переменные (искомые величины) данной задачи?
2. Какие ограничения должны быть наложены на переменные, чтобы выполнить условия, характерные для моделирования системы?
3. В чём состоит цель, для достижения которой из всех допустимых значений переменных нужно выбрать те, которые будут соответствовать оптимальному (наилучшему) решению задачи?
Выразим словесно суть проблемы (словесная формулировка задачи):
Фирме требуется определить объёмы производства (т) каждой из красок, максимизирующие доход (тыс. руб.) от реализации продукции с учётом ограничений на спрос и расход исходных продуктов.
Трудность построения ММ заключается в идентификации переменных и последующем представлении цели и ограничений в виде математических выражений этих переменных.
Переменные
Так как нужно определить объёмы производства каждого вида краски, то переменными в модели являются:
Х1 - суточный объём производства краски Н, т;
Х2 - суточный объём производства краски В, т.
Целевая функция
Так как стоимость 1 т краски Н равна 3 тыс. руб., суточный доход от её продажи составит 3х 1 тыс. руб.
Аналогично доход от реализации х2 т краски В составит 2х2 тыс. руб. При допущении независимости объёмов сбыта каждой из красок общий доход равен сумме двух слагаемых - дохода от продажи краски Н и дохода от продажи краски В.
Обозначив общий доход (в тыс. руб.) через F, можем дать следующую математическую формулировку целевой функции:
Определить (допустимые) значения х1 и х2, максимизирующие величину общего дохода
F = 3 х1+2 х2.
Ограничения
При решении рассматриваемой задачи должны быть учтены ограничения на расход исходных продуктов и спрос на изготовление краски.
Ограничения на расход имеют вид:
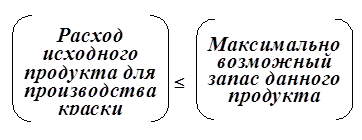
это приводит к следующим двум ограничениям:
х1 + 2х2 £ 6 (для А);
2х1 + х2 £ 8 (для В).
ограничение на величину спроса на продукцию имеет вид:

 Превышение спроса на
Превышение спроса на
 краску В относительно 1 т/сут.
краску В относительно 1 т/сут.
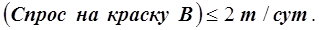
Математически эти ограничения записываются следующим образом:
х2 - х1 £ 1 (соотношение спроса на краску В и краску Н);
х2 £ 2 (максимальная величина спроса на краску В).
Неявное (т.е. подразумеваемое) ограничение заключается в том, что объёмы производства продукции не могут принимать отрицательные значения (т.е. быть меньше нуля). Потребуем выполнения условия неотрицательности переменных, т.е. введём ограничение на знак:
Х2 ³ 0 (объём производства краски В);
Х1 ³ 0 (объём производства краски Н)
(или "х ³ 0).
Итак, ММ можно записать так:
Определить суточные объёмы производства (х2 и х1) краски В и краски Н (в т), при которых достигается
F = 3 х1 + 2 х2 ® max.
при
 x1 + х2 £ 6,
x1 + х2 £ 6,
2х1 + х2 £ 8,
- х1 + х2 £ 1,
х2 £ 2
"х ³ 0
Целевая функция и ограничения - линейные.
Линейность предполагает наличие двух свойств:
- пропорциональности;
- аддитивности.
Пропорциональность означает, что вклад каждой переменной в целевую функцию и общий объём потребления соответствующих ресурсов прямо пропорционален уровню этой переменной. Если, например, фирма будет предоставлять скидку покупателям, скажем, продавая краску Н по цене 2,5 тыс. руб. за 1 т при объёме закупок свыше 2 т, то в такой ситуации не будет выполняться исходное условие задачи, заключающееся в том, что производство одной тонны краски Н обеспечивает доход от реализации, равный 3 тыс. руб. В новых условиях этот доход будет равен 3 тыс. руб. при х1 £ 2 т и 2,5 тыс. руб. при х1>2, т.е. прямая пропорциональность между доходом фирмы и величиной х1 не имеет места.
Аддитивность заключается в том, что целевая функция представляет собой сумму вкладов от различных переменных.
Аналогично левая часть каждого ограничения должна представлять собой сумму расходов, каждое слагаемое которой пропорционально величине соответствующей переменной. Если фирма производит два конкурирующих вида продукции, увеличение сбыта одного из которых отрицательно сказывается на объёме реализации другого, то такая ММ не обладает свойствами аддитивности.
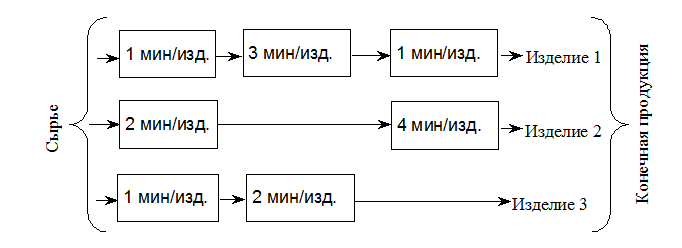
Пример 1.5. (Задача об ассортименте продукции.) Фирма выпускает три вида продукции (изделий). В процессе производства используются три технологические операции. На рис. 1.1 показана технологическая схема производства изделий видов 1, 2 и 3. При изготовлении изделия 2 технологическая операция 2 не выполняется, а при производстве изделия 3 используются только технологические операции 1 и 2.
 2014-02-09
2014-02-09 957
957