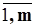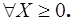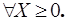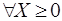При решении задач планирования и управления процессами перевозок на железнодорожном транспорте на основе компьютерной технологии особое место занимают методы оптимизации. Процесс оптимизации предполагает выбор такого варианта, при котором достигается экстремальное значение критерия оптимизации, характеризующего качество управления.
Можно выделить целый класс задач оптимизации, когда при нахождении экстремума критерий оптимизации (целевая функция) и ограничения являются линейными функциями.
В таком случае задача нахождения экстремума носит специфическое название задачи линейного программирования (ЛП).
Различные задачи оптимального управления и планирования на железнодорожном транспорте можно свести к моделям ЛП.
ЛП позволяет изучать задачи нахождения оптимального (наилучшего) значения линейной целевой функции F при линейных ограничениях на параметры управления - переменные задачи.
Общей задачей ЛП (ОЗЛП) называется задача, состоящая в определении оптимального (max или min, одним словом - extr) значения F целевой функции: F =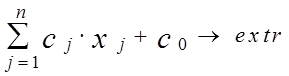 (1.1)
(1.1)
при условиях (ограничениях):
|
|
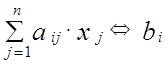
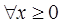 , (1.3)
, (1.3)
где aij, cj, bi - вещественные числа, символ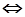 - один из знаков отношений
- один из знаков отношений 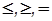 .
.
Следовательно, в ОЗЛП отыскивается extr целевой функции (1.1) на множестве решений системы равенств и неравенств (1.2) при условии неотрицательности некоторых переменных. Отметим, что требование неотрицательности (1.3) может быть наложено на все переменные (L={1,2,...,n}) или вообще отсутствовать (L=0).
Совокупность чисел X =(x1 , x2 ,..., xn), удовлетворяющую ограничениям (1.2), (1.3) называют допустимым решением или планом.
План X*=(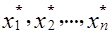 ), при котором целевая функция принимает
), при котором целевая функция принимает
экстремальное значение, называется оптимальным.
Таким образом, при любом плане X оптимальный план X* удовлетворяет условию: F(X*) F(X) или F(X*)
F(X) или F(X*)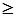 F(X).
F(X).
Не всякая задача ЛП имеет оптимальный план. Это связано с тем, что множество решений D системы ограничений (1.2), (1.3) может быть пустым или форма F на D не ограничена сверху или снизу.
Например: 1. Для ОЗЛП найти max целевой функции F = x1 + x2 при ограничениях:
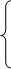 x1+x2
x1+x2 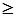 3,
3, 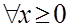 .
.
x1 1,
1,
x2 1.
1.
Здесь D=0, поскольку ограничения противоречивы, оптимальный план отсутствует.
2. Для ОЗЛП найти min целевой функции F = x1 + 2x2 при ограничениях:
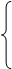 x1+x2
x1+x2  2,
2,
-x1+x2 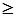 5,
5,
x2 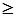 0.
0.
При 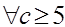 пара X1= - C, X2 = 0 является планом, однако F не ограничена снизу, поэтому оптимальный план отсутствует.
пара X1= - C, X2 = 0 является планом, однако F не ограничена снизу, поэтому оптимальный план отсутствует.
Среди множества задач ЛП выделяют класс так называемых канонических, или основных задач, в которых находится min F целевой функции (1.1) при ограничениях (1.2), (1.3) где 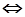 есть =.
есть =.
Иными словами, в канонической задаче ЛП (КЗЛП) находится min F на множестве решений системы уравнений при неотрицательности всех параметров (переменных) задачи.
Несложными преобразованиями нахождение основных задач ЛП (ОЗЛП) всегда может быть сведено к решению некоторой КЗЛП.
Покажем, как это делается.
1. Прежде всего нахождение max F заменяется нахождением min F,
т.е. max F= - min (-F).
2. Всякое ограничение в задаче ЛП вида

|
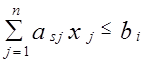 ,
, заменяется условием - равенством с неотрицательностью новой вспомогательной переменной xn+i, которую следует интерпретировать как остаток, или неиспользованную часть данного ресурса, если исходное ограничение определяет расход некоторого продукта.
|

|
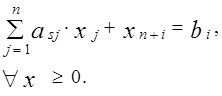
 3. Ограничение вида
3. Ограничение вида 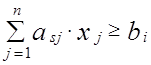 , i =1,m необходимо преобразовать, так как левая часть этого ограничения не может быть меньше правой. Для обращения исходного неравенства в равенство вычтем из его левой части избыточную переменную xn+ i > 0. В результате имеем:
, i =1,m необходимо преобразовать, так как левая часть этого ограничения не может быть меньше правой. Для обращения исходного неравенства в равенство вычтем из его левой части избыточную переменную xn+ i > 0. В результате имеем:
|
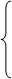

|
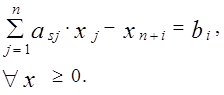
Замечание. 1. Правую часть равенства всегда можно сделать неотрицательной, умножая обе части на -1. Например, равенство
2x1 + 3x2 -7x3 = -5 эквивалентно равенству -2x1 - 3x2 +7x3 = 5.
2. Знак неравенства изменится на противоположный при умножении обеих частей на -1. Например, можно вместо 2 < 4 записать -2 > -4, неравенство 2x1 - x2 £ -5 заменить на -2x1 + x2 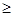 5.
5.
4. Переменные Xp , на которые не наложены условия неотрицательности, представляются в (1.1) и (1.2) в виде разности неотрицательных величин:
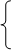 Xk=Wk - Vk,
Xk=Wk - Vk,
Wk 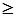 0; Vk
0; Vk 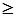 0.
0.
Важная особенность переменных Wk и V k состоит в том, что при любом допустимом решении только одна из переменных может принимать положительное решение, т.е. если Wk >0, то X k = 0, и наоборот. Это позволяет рассматривать Wk как остаточную переменную, а X k - как избыточную, причем лишь одна из этих переменных может принимать положительное значение.
После всех этих преобразований удобно опять переобозначить Wk на X k , а другие вспомогательные неизвестные заменить на X n+1, X n+2,..., X n+t, где t есть сумма количества неравенств в (1.2) и количества переменных без ограничений. Тогда мы получим следующую КЗЛП.
Найти новую линейную форму min F1 (1.6)
при ограничениях:
|
|


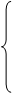
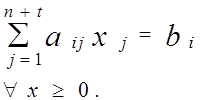 , i= 1, m; j= 1, n+t
, i= 1, m; j= 1, n+t Заметим, что каждому плану X* (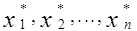 ) (1.7)
) (1.7)
задачи (1.1), (1.2), (1.3) можно поставить в соответствие некоторый план:
 X* (
X* (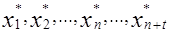 )(1.8)
)(1.8)
задачи (1.6), (1.6*), (1.6**), где числа 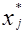 (j= 1, n+t) получаются по той же схеме, по которой реализовывался переход от ОЗЛП к КЗЛП. Имея план (1.8) для задачи (1.4), (1.5), (1.6) можем получить план (1.7) для (1.1), (1.2), (1.3), элементы которого равны соответствующим элементам (1.8) или их некоторым разностям. Последнее имеет место при наличии в ОЗЛП переменных без ограничений.
(j= 1, n+t) получаются по той же схеме, по которой реализовывался переход от ОЗЛП к КЗЛП. Имея план (1.8) для задачи (1.4), (1.5), (1.6) можем получить план (1.7) для (1.1), (1.2), (1.3), элементы которого равны соответствующим элементам (1.8) или их некоторым разностям. Последнее имеет место при наличии в ОЗЛП переменных без ограничений.
Нетрудно убедиться, что кроме полученного взаимно однозначного соответствия между планами ОЗЛП и КЗЛП значение целевой функции F на соответствующих планах одинаковы. Таким образом, оптимальному решению задачи (1.1), (1.2), (1.3) соответствует оптимальное решение (1.6), (1.6*), (1.6**). В этом смысле указанные задачи эквивалентны.
Пример 1.1. Записать в форме КЗЛП следующую ОЗЛП:
Найти max целевой функции F= 3x1 – 2x2 – 5x4 + x5 при ограничениях
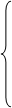 2x1+ x3 - x4 + x5
2x1+ x3 - x4 + x5  2,
2,
x1 - x3 + 2x4 + x5  3,
3,
2x2 + x3 - x4 + 2x5  6,
6,
x1 + x4 - 5x6 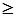 8.
8.
|
Решение. В данной задаче требуется найти max F, а система ограничений содержит четыре неравенства. Следовательно, чтобы записать ее в форме КЗЛП нужно:
1. Вместо нахождения max F записать F1 = -F.
2. Перейти от ограничений-неравенств к ограничениям-равенствам.
Так как число неравенств, входящих в систему ограничений нашей задачи, равно четырем, то этот переход может быть осуществлен введением четырех дополнительных неотрицательных переменных. При этом к левым частям каждого из неравенств вида “  ” соответствующая дополнительная переменная прибавляется, а из левых частей каждого из неравенств вида “
” соответствующая дополнительная переменная прибавляется, а из левых частей каждого из неравенств вида “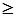 ” вычитается.
” вычитается.
Следовательно, исходная задача может быть записана в форме КЗЛП таким образом:
- минимизировать функцию F= - 3X1 + 2X2 + 5X4 - X5
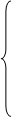 2X1+ X3 - X4 + X5 + X6 = 2,
2X1+ X3 - X4 + X5 + X6 = 2,
X1 - X3 + 2X4 + X5 + X7 = 3,
2X2 + X3 - X4 + 2X5 +X8 = 6,
X1 + X4 - 5X6 - X9 = 8,
|
Пример 1.2. записать в форме КЗЛП следующую ОЗЛП. Найти max целевой функции F = X1 + X2 - X3 при ограничениях
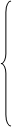 2X1 - X2 - X3 + X4
2X1 - X2 - X3 + X4  6,
6,
X1+ 2X2 + X3 - X4 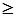 8,
8,
3X1 - X2 + 2X3 + 2X4  10,
10,
- X1+ 3X2 + 5X3 - 3X4 = 15.
|
Решение. В данной задаче требуется найти max F, а система ограничений содержит три неравенства. Следовательно, чтобы записать ее в форме КЗЛП, нужно составить нахождение min F при ограничениях, полученных из исходной задачи добавлением к левым частям каждого из неравенств вида “  ” дополнительной неотрицательной переменной и вычитанием дополнительных переменных из левых частей каждого из ограничений-неравенств вида “
” дополнительной неотрицательной переменной и вычитанием дополнительных переменных из левых частей каждого из ограничений-неравенств вида “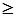 ” за исключением четвертого уравнения.
” за исключением четвертого уравнения.
Следовательно, исходная задача может быть записана в КЗЛП так:
Найти min F=-X1 + 2X2 - X3 + X4
при условиях
 2X1 - X2 - X3 + X4 + X5 = 6,
2X1 - X2 - X3 + X4 + X5 = 6,
X1 + 2X2+ X3 - X4 - X6 = 8,
3X1 - X2 + 2X3+2X4 + X7 = 10,
- X1 +3X2 +5X3 - 3X4 = 15.
 2014-02-09
2014-02-09 1016
1016