УДК 517.8
Конспект лекций
Компьютерный практикум по организации и управлению на железнодорожном транспорте
Ростов – на – Дону
Компьютерный практикум по организации и управлению на железнодорожном транспорте / А.И. Филоненков 2-е изд., перераб. И доп.; Рост. гос. ун-т путей сообщения. Ростов н/Д, 2003
В конспекте лекций по компьютерному моделированию излагаются приемы и методы решения задач транспортной тематике
Рекомендовано к изданию комиссией УМО
'' Применение ВТ в учебном процессе и научных исследованиях ''.
Предназначено для студентов факультета УПП, АТС и слушателей ФПК.
Табл. Ил. Библиограф. 7 назв.
Рецензенты: канд. тех. наук проф. Н.Г. Мищенко (РГУПС);
зам. нач. ИВЦ, доц. Э.В. Тучков (СКЖД)
© Ростовский государственный путей сообщения, 2003
I.I. Основные положения
Создание математических моделей производственных процессов с целью получения наилучших экономических показателей в настоящее время становится основной рациональной организации производства, особенно на железнодорожном транспорте. Роль моделирования возрастает в тех случаях, когда управление производственным процессом осуществляется с ЭВМ.
Знание основ моделирования и оптимизации необходимо инженерам, плановикам, организаторам и руководителям различного масштаба, ранее не сталкивающими с такими предметами, как вычислительная техника, математическое моделирование и математическая теория оптимизации. Однако почерпнуть необходимые сведения по этим вопросам подчас довольно трудно, так как книги по моделированию и оптимизации написаны на высоком теоретическом уровне и не под силу студентам и слушателям ФПК. Основы моделирования и оптимизации им нужно преподносить в максимально простой форме.
Прежде всего читателя необходимо ознакомить с основными положениями и терминами моделирования. Рассмотрим, что же такое система, на какие виды они подразделяются, как функционируют.
Системой называют совокупность совместно действующих в пространстве и во времени объектов, предназначенных для выполнения заданных функций. Различают технические и производственные системы.
Технические системы – это машины, аппараты, приборы, ЭВМ, станки и т.д. Производственные системы представляют собой структуры, в которых происходит измерение, обработка и преобразование различных вещественных потоков. К ним относятся железные дороги и их линейные подразделения, в промышленности – заводы и их цеха и т.д.
При создании и эксплуатации систем необходимо знать течение рабочего процесса в системе, или ее функционирование.
Рабочие процессы обычно бывают сложными и не всегда поддаются теоретическим расчетам. Исследование таких процессов сопряжено со значительными трудностями. Нередко бывает так, что те или иные свойства и характеристики, трудно обнаруживаемые в каких- либо системах, процессе или явлении, сравнительно заметно проявляются в других системах, процессе или явлении, сходных с первыми по определенным признакам. Это дает возможность использования в процессе исследования методов аналогии и моделирования. По сути дела, при объяснении сложных явлений мы ищем сходство, аналогии с тем, что нам уже известно, т.е. мы стремимся к объяснению неизвестного, непонятного через известное, понятное. Аналогии определяют как сходство (подобие) в определенном отношении между различными предметами или явлениями в зависимости от этого подразделяют на функциональные, структурные и аналогии внешней формы.
Чтобы воспользоваться функциональной аналогией, нужно определить, какие функции должен выполнять объект, а потом искать, кто или что в окружающем мире выполняет подобные функции.
Использовать структурной аналогии предполагает поиск в окружающем мире структур, аналогичных примерным, которые наилучшим образом выполняли бы поставленную задачу. Например, многоярусные башни В.Г. Шухова подобны строению стебля растений.
Когда вновь создаваемый объект по внешнему виду делается подобным какому- то другому, уже известному, свойства которого мы хотим получить, то используют аналогию внешней формы.
Объективное основание для такого логического переноса признаков с известного нам объекта на неизвестный основывается на том положении, что свойства любой системы существуют не изолированно одно от другого. Они тесно взаимосвязаны, причем изменение любого существенного признака сказывается и на других признаках. Это дает предполагать, что если два объекта наблюдения обладают одинаковой совокупностью определенных свойств, то и другой объект должен обладать этими же свойствами.
Однако, делая умозаключение или выводы на основе аналогии, нужно помнить, что эти выводы не являются абсолютно достоверными, истинными, а носят лишь более или менее вероятностный характер и поэтому нуждаются дополнительной проверке. Пользуясь методом аналогии, очень важно исследовать не только свойства объектов, но и сцепить их возможное влияние на прогнозируемые свойства изучаемого объекта.
Важную роль в исследовании сложных динамических систем (такие системы называют кибернетическими) играет метод моделирования. Моделирование – это метод исследование на моделях или на реальных установках с применением методов теории подобия при постановке эксперимента и обработке его результатов.
Модель представляет собой искусственный, созданный исследователем объект любой природы (материально реализованный или умозаключи тельный), который замещает или воспроизводит изучаемый объект так, что исследование модели способно давать новую информацию об этом объекте.
С точки зрения информации модель – информационное отражение (образ) системы оригинала (прообраза) в соответствии с данной целью моделирования.
Моделирование как метод исследования основано на способности человека абстрагировать сходные признаки или свойства у различных объектов между ними определенные соответствия.
Моделирование имеет весьма большое сходство с методом аналогии и рассматривается как разновидность и дальнейшее развитие последнего. Говорят о сходстве (аналогии) модели с оригиналом, нужно всегда помнить, что они не тождественны друг другу, т.е. между моделью и оригиналом на ряду со сходством обязательно имеются более или менее существенные различия. Поэтому и суждения о структуре или поведения оригинала, сделанные на основе изучения его модели, или заключения по аналогии носят не абсолютно достоверный, а более или менее приблизительный характер. Окончательные выводы требуют дальнейшего уточнения, конкретизации и корректировки.
Однако, несмотря на относительность и не абсолютную достоверность заключений об исследуемом оригинале, метод моделирования широко используется в качестве одного из важнейших методов исследования систем.
I.2. Основные виды моделей
Различают следующие виды моделей: геометрические, физические и математические.
Геометрические модели представляют некоторый объект, геометрически подобный своему оригиналу, дают внешнее представление о нем и большей частью служат для демонстрационных целей (макеты вокзалов, парков, станций и т.д.). Эти модели, как правило, выполняются в другом масштабе, а в ряде случаев и с изменением мерности пространства (двумерная плоская карта, карта трехмерной местности, двумерный чертеж трехмерной детали, плоский рисунок и фотографии трехмерных объектов и т.д.).
В основе построения этих моделей без изменения мерности пространства лежит определение подобия геометрических объектов: два геометрических объекта считаются подобными, Ю если при соответствующем взаимном расположении можно добиться их совпадения при однородной деформации линейных размеров, т.е. при изменении всех размеров в одно и то же число раз.
Поскольку при построении этих моделей основную роль играет их геометрическое подобие, а не процессы функционирования, то, естественно, в кибернетике, изучающей процессы управления, эти модели могут иметь лишь подсобное значение.
Физические модели в технике имеют более важное значение, чем геометрические. Они отражают подобие между оригиналом и моделью не только с точки зрения их формы и геометрических соотношений, но и основных физических процессов. Физически подобными называются явления в геометрически подобных системах, у которых в процессе их функционирования отношения характеризующих их одноименных физических величин в сходственных точках являются постоянной величиной. При физическом моделировании модель и ее прототип всегда являются объектами, имеющими одинаковую физическую природу.
При исследовании на физических моделях в соответствии с геометрическими размерами модели изменяются и другие физические параметры. Так, при построении модели плотины в I/I0 натуральной величины в I0 раз уменьшается и давление на нее воды и т.д.
Математические модели являются наиболее универсальными. Если математические выражения, описывающие различные физические явления, одинаковы по форме записи и отличаются лишь физическим смыслом, входящим в эти выражения, то такие выражения называются математическими изоморфными, математический изоморфизм позволяет изучать поведение одних физических систем с помощью других, причем качественные и количественные параметры этих систем также изоморфны.
Математическими называют такое моделирование, при котором физические процессы в оригинале и модели протекают по законам изоморфизма, т.е. по одинаковым математическим законам, хотя физическая природа процессов может быть различна. Следовательно, математическим моделированием называют описание процесса или явления с помощью математических зависимостей.
Важным этапом изучения явлений, процессов является их систематизация, результатом которой обычно является классификация, производимая по некоторым признакам, выбираемым исследователем. Поскольку признаков очень много, то и классификации могут различаться. Каждая из них должна преследовать определенную цель. Так как для задач распределения ресурсов принимаются решения с помощью ЭВМ на основе математических моделей, цель нашей классификации заключается в их систематизации, потому что для разных математических моделей их алгоритмы, а следовательно, и программное обеспечение, являющиеся основой решения задачи на ЭВМ, различаются.
В известной задаче линейного программирования (ЛП)
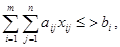
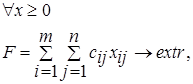
в качестве элементов модели можно рассматривать параметры сij, aij, bi; переменные xij; зависимости между параметрами и переменными. Возможные виды каждого элемента приведены на рис. 4.

 2014-02-09
2014-02-09 2519
2519
