.
Третья задача анализа на чувствительность отвечает на вопрос: в каких пределах допустимо изменение коэффициентов целевой функции?
Изменение коэффициентов целевой функции оказывает влияние на наклон прямой, которая представляет эту функцию в принятой системе координат (графический метод). Вариация коэффициентов целевой функции может привести к изменению совокупности связывающих ограничений и, следовательно, статуса того или иного ресурса, т.е. сделать недефицитный ресурс дефицитным и наоборот. Следовательно, в рамках анализа модели на чувствительность к изменению коэффициентов целевой функции могут исследоваться следующие вопросы:
- каков диапазон изменения (увеличения или уменьшения) того или иного коэффициента целевой функции, при котором не происходит изменения оптимального решения?
- насколько следует изменить тот или иной коэффициент целевой функции, чтобы сделать некоторый недефицитный ресурс дефицитным и, наоборот, дефицитный ресурс сделать недефицитным?
Рассмотренные задачи характеризуют основные принципы анализа моделей на чувствительность после нахождения оптимального решения.
Более подробно эти вопросы изложены в [2], [5].
Используя геометрическую интерпретацию, найдите решение следующих задач:
|
|
|
|
|
|
|
|
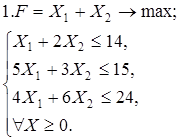
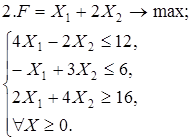
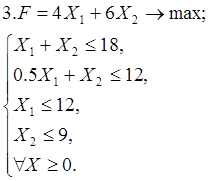
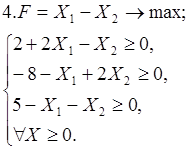
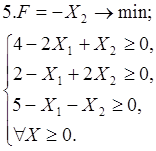
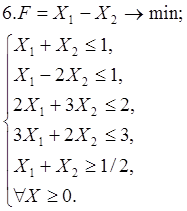
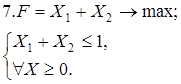
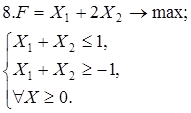
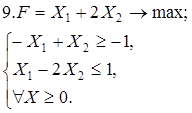
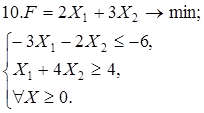
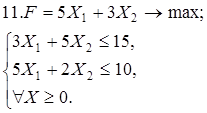
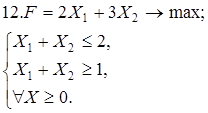
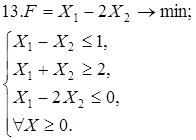
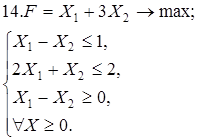
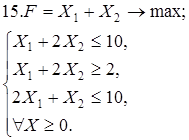
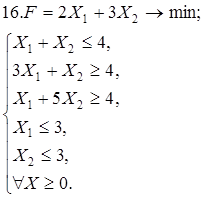
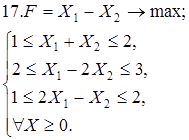
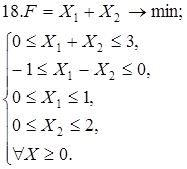
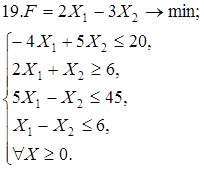
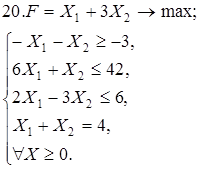
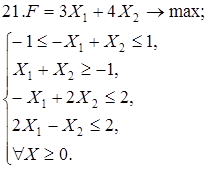
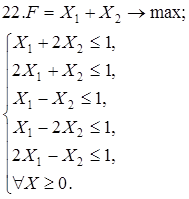
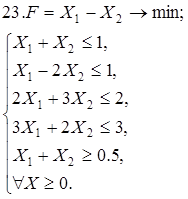
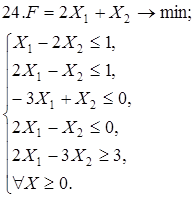
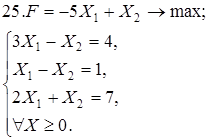
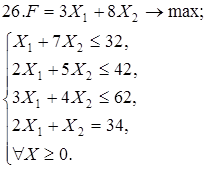
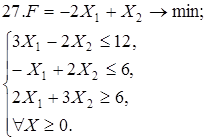
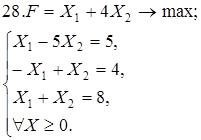
Каноническая задача имеет смысл только тогда, когда n (число неизвестных переменных) больше m (числа уравнений).
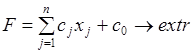 (1.17)
(1.17)
при условиях (ограничениях)
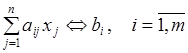 (1.18)
(1.18)
"x ³ 0. (1.19)
Если число уравнений больше числа неизвестных, то либо эти уравнения линейно зависимы, и тогда часть из них можно отбросить, либо эти уравнения противоречивы, и не существует ни одного допустимого решения. Если же число линейно-независимых уравнений равно числу неизвестных, то существует единственное решение, и поэтому не возникают задачи отыскания экстремума. Условие n>m в канонической задаче обусловливает множество решений системы. Среди множества решений существуют так называемые базисные решенияXб. Они строятся следующим образом. Среди n неизвестных выбирают m (по числу уравнений). Эти m неизвестных образуют базис. Все остальные n-m неизвестные, не вошедшие в число отобранных, полагают равными нулю и называют небазисными (свободными) неизвестными. Существует множество вариантов выбора базиса. Число таких вариантов равно 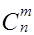 . Базисное решение системы уравнений будет допустимым (опорным), если все базисные переменные неотрицательны (Xj
. Базисное решение системы уравнений будет допустимым (опорным), если все базисные переменные неотрицательны (Xj 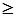 0). Таким образом, допустимым решением (планом) называют любой набор переменных X j, удовлетворяющих ограничениям (1.18) и (1.19).
0). Таким образом, допустимым решением (планом) называют любой набор переменных X j, удовлетворяющих ограничениям (1.18) и (1.19).
Решение задачи ЛП заключается в том, чтобы среди всех опорных базисных решений выбрать такое, при котором целевая функция (1.17) достигает экстремума. Наиболее распространенным методом решения задач ЛП канонического вида является симплекс-метод. Симплекс-метод заключается в последовательном вычислении решений, находящихся в вершинах многогранника (симплекса), образующего область допустимых решений. Вычисления выполняются таким образом, что значения целевой функции при каждом следующем шаге строго возрастают. Это свойство симплекс-метода приводит к тому, что просматривается лишь небольшая часть допустимых решений из общего числа. Благодаря этому за приемлемое время можно решить задачи с большим числом переменных.
Целенаправленный переход от одного допустимого решения к другому (от одной вершины симплекса к другой) осуществляется при этом за счет изменения состава базисных и свободных переменных по специальным правилам замещения.
Основная система уравнений
Пусть Xб = 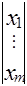 ³ 0 - базисный вектор, X =
³ 0 - базисный вектор, X = 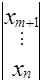 ³ 0 - небазисный вектор,
³ 0 - небазисный вектор,
B = 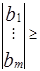 0 - вектор свободных членов, A =
0 - вектор свободных членов, A =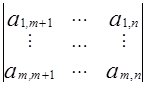 - матрица коэффициентов.
- матрица коэффициентов.
Основной или нормальной формой системы уравнений называется векторное уравнение вида
Xб = B – AX, (1.20)
которое в координатной форме имеет вид:
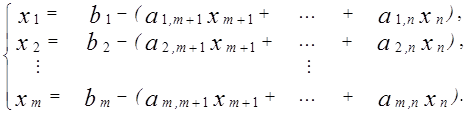 (1.21)
(1.21)
По определению выполняется соотношение m<n, т.е. число уравнений всегда меньше числа неизвестных.
В системе (1.21) можно разрешить любое уравнение относительно любой переменной и подставить ее во все уравнения. Тогда получим новую систему уравнений, равносильную данной. Но вся система не обязательно удовлетворяет условиям основной системы. Из всех тождественных линейных преобразований можно выбрать такое, которое является инвариантным относительно свойства быть основной системой (инвариант-математическое выражение, остающееся неизменным при определенном преобразовании переменных, связанных с этим выражением). Такие преобразования называются нормальными исключениями или симплекс-преобразованиями, которые определяются следующими операциями.
1. Выбираем такой столбец матрицы А, который имеет хотя бы один положительный элемент aij. Такой столбец называют разрешающим. Пусть для простоты рассуждения он будет первым в системе (1.21).
2. В разрешающем столбце для всех положительных элементов находим множество частных от деления на них соответствующих членов, т.е. находим для 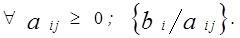
3. Из полученного множества выбираем наименьший положительный элемент. Строку, в которой это реализовалось, назовем разрешающей. Положим, для определенности, что эта строка будет первая в системе (1.21).
4. Элемент матрицы А, стоящий на пересечении разрешающей строки и разрешающего столбца, назовем разрешающим. В нашем случае это 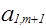 .
.
Решим уравнение системы относительно неизвестного, стоящего при разрешающем элементе.
5. Подставим найденное значение неизвестного во все другие уравнения, получим систему
|
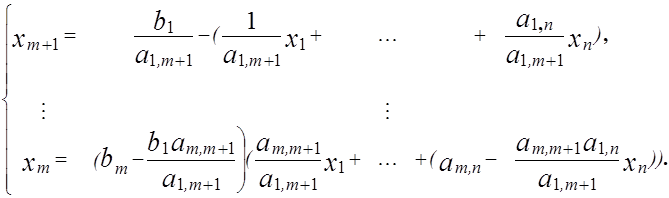
В результате исходная система (1.21) преобразована в новую систему (1.22), в которой произошло замещение переменной в базисном векторе. Все вычисления значительно упрощаются, если использовать компактный способ записи в специального рода таблицах. В таблице записывается только числовая информация системы (1.21), а в заголовке указывается, к каким переменным эта информация относится (табл. 1.7).
Таблица 1.7
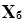 | B | Xc | ||
| xm+ 1 | ... | xn | ||
| x 1 | b 1 | a 1 ,m+ 1 | ... | a 1 ,n |
| ... | ... | ... | ... | ... |
| xm | bm | am,m+ 1 | ... | am,n |
Правила образования новых коэффициентов при замещении базиса
приведены в табл. 1.8.
 2014-02-09
2014-02-09 1106
1106

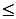 10, X1 + 2X2
10, X1 + 2X2 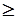 2, 2X1 + X2
2, 2X1 + X2 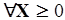 .
. 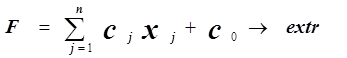 (1.17) при условиях (ограничениях)
(1.17) при условиях (ограничениях) 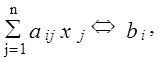 i=
i= 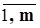 (1.18)
(1.18) 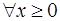 . (1.19)
. (1.19)