Проверка задач ЛП на чувствительность

Таблица 1.5

	Вагоны
	Багажные	Почтовые	Плацкартные	Купейные	Мягкие
Парк вагонов
Состав скорого поезда		---
Состав пассажир-ского поезда

Для составления математической модели перевозочного процесса введем обозначение: X₁ - число скорых поездов, Х₂ - число пассажирских поездов. Тогда, ограничивающие неравенства, вытекающие из табл. 1.5 будут иметь вид:

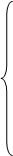X₁ + X₂ 14,ограничение по багажным вагонам

(1.14)

X₂ 10,,ограничение по почтовым вагонам

10 X₁ + 8 X₂ 120,,ограничение по плацкартным вагонам

7X₁ + 5 X₂ 70,,ограничение по купейным вагонам

(1.15)

4X₁ + 2X₂ 28,,ограничение по мягким вагонам

.

Таблица 1.6

	Вагоны
Багажный	Почтовый	Плацкартный	Купейный	Мягкий
Число перевозимых пассажиров	---	---

Обозначим целевую функцию через F. Основные принципы определения целевой функции изложены в [1, 2]. В нашей задаче целевая функция определяет число перевозимых пассажиров и, учитывая данные табл. 1.6, получим

F=(56·10+36·7+24·4)X₁+ (56·8+36·5+24·2)X₂ =

= 908X₁ + 676X₂ max. (1.16)

Целевая функция составлена корректно, поскольку она отвечает принципам однозначности (стремится к max), соответствия, управляемости (целевая функция выражена через параметры управления Х₁, Х₂). Далее поступаем согласно алгоритму, изложенному выше. Строим ОДР в системе координат Х₂OХ₁, для этого построим граничные прямые:

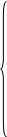X₁ + X₂ = 14,

X₂ = 10,

10 X₁ + 8 X₂ = 120,

7X₁ + 5 X₂ = 70,

4X₁ + 2X₂ = 28,

" X ³ 0.

Эти прямые изображены на рис. 1.7. Каждая из построенных прямых делит плоскость на две полуплоскости. Координаты точек одной полуплоскости удовлетворяют исходному неравенству, а другой - нет. Чтобы определить искомую полуплоскость, нужно взять какую-нибудь точку, принадлежащую одной из полуплоскостей и проверить, удовлетворяют ли ее координаты данному неравенству. Если координаты взятой точки удовлетворяют неравенству, то искомой является полуплоскость, которой принадлежит эта точка, в противном случае - другая полуплоскость. Найдем, например, полуплоскость, определяемую неравенством

X₁ + X₂ 14. Для этого, построив прямую Х₁ +Х₂ =14 (на рис. 1.7 это прямая I), возьмем какую-нибудь точку, принадлежащую одной из двух полученных полуплоскостей, например точку О(0,0). Координаты этой точки удовлетворяют неравенству 0+0<14; отсюда следует, что полуплоскость, которой принадлежит точка О(0,0), определяется неравенством X₁ + X₂ 14. Это и показано стрелками на рис. 1.7. Пересечение полученных полуплоскостей и определяет ОДР исходной задачи.

Как видно из рис. 1.7, ОДР - это многоугольник OАВС.

Координаты любой точки, принадлежащей ОДР, удовлетворяют данной системе неравенств и условию неотрицательности переменных, поэтому сформулированная задача будет решена, если сможем найти точку, принадлежащую ОДР, в которой функция F принимает max.

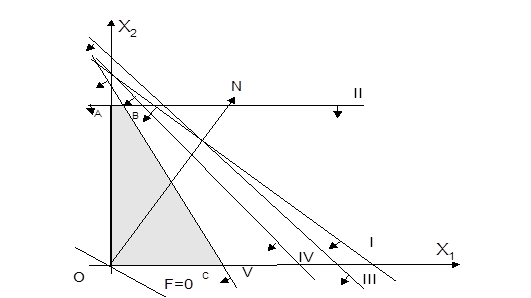
Рис. 1.7

Чтобы найти указанную точку, можно воспользоваться двумя способами:

1. Построим вектор 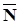(908, 676)=100(9,08; 6,76), указывающий направление возрастания F, и через начало координат проводим прямую, перпендикулярную нашему вектору.

2. Либо полагаем, что X₁ равняетсякакому-либо числу (например

X₁ = 10) и, подставив это значение в уравнение F: 908 X₁ + 676 X₂ =0 (9080+676X₂ =0), решаем его: X₂ = - 13,43; проводим прямую через начало координат и точку L (10, - 13,43), это и будет искомая прямая F.

Перемещая построенную прямую любым из перечисленных выше способов в направлении вектора 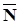, видим, что последней общей точкой ее с ОДР служит точка В. Координаты этой точки и определяют число

скорых и пассажирских поездов, которые перевезут максимальное число пассажиров.

Точка В лежит на пересечении прямых Х₂=10 (II) и 4Х₁+2Х₂=28 (V). Для определения ее координат решим систему уравнений:

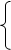Х₂=10,

4Х₁+2Х₂=28.

Получим Х₁*=2; X₂*=10; X₁*, X₂* - оптимальные решения.

Подставим значения Х₁* и Х₂* в функцию цели, получим Fmax=908·2+676·10=8576 пассажиров.

Из рис. 1.7 видно, что прямые 7Х₁+5Х₂=70и10Х₁+8Х₂=120 находятся вне ОДР и практически не вносят ограничений в задачу. С математической точки зрения эти условия являются лишними, а с точки зрения планирования - это резерв по этим типам вагонов, который может быть использован для других целей.

Следовательно, при назначении 2 скорых и 10 пассажирских поездов max число перевозимых пассажиров составит 8576.

В том случае, когда железная дорога не в состоянии пропустить расчетное число поездов, т.е. имеются ограничения по пропускной способности, то в систему ограничений следует включить дополнительное неравенство. Далее поступают по изложенному выше алгоритму.

Пример. Найти max F=2X₁+3X₂ при следующих ограничениях:

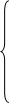2X₁ + X₂ 10,

- 2X₁ +3X₂ 6,

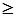2X₁ + 4X₂ 8,

" X ³ 0.

Строим граничные прямые:

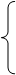2X₁ + X₂ = 10,

- 2X₁ + 3X₂ = 6,

2X₁ + 4 X₂ = 8.

Эти прямые изображены на рис. 1.8.

Для построения прямой F=2X₁+3X₂=0 можно воспользоваться любым из способов: либо строим радиус-вектор N(2,3), указывающий направление возрастания F, и через точку О проводим прямую, перпендикулярную ему, либо, положив X₁ = -3, найдем X₂, решив уравнение

- 6 + 3X₂ = 0. Отсюда следует, что X₂ = 2, строим F через точки O(0,0) и K(-3,2).

Построенную прямую F=0 перемещаем параллельно самой себе в направлении вектора N. Из рис. 1.8 видно, что опорной по отношению к

ОДР эта прямая становится в точке С, где F достигает max. В точке С пересекаются две прямые I и II, имеющие следующие уравнения:

2Х₁ + Х₂ = 10 и - 2Х₁ + 3Х₂ = 6.

Решая систему указанных уравнений, находим Х₁* =3; X₂* =4,

откуда F = 2•3+3•4 = 18. Следовательно, при плане

Х* =(Х₁*, Х₂*) = (3,4) значение целевой функции составит F max = 18.

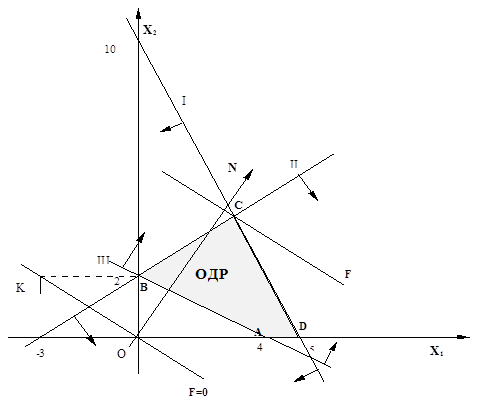
Рис. 1.8

В заключение рассмотрим анализ ММ на чувствительность. Этот анализ выполняется после нахождения оптимального решения. В рамках такого анализа выявляется чувствительность оптимального решения к определённым изменениям исходной модели.

При анализе рассматривается некоторая совокупность линейных оптимизационных моделей. Это придаёт модели определённую динамичность, позволяющую исследователю проанализировать влияние возможных изменений исходных условий на полученное ранее оптимальное решение. Динамические характеристики моделей фактически отображают аналогичные характеристики, свойственные реальным процессам.

Рассмотрим три простые задачи анализа на чувствительность.

Первую задачу можно сформулировать так: на сколько сократить или увеличить запасы ресурсов? После нахождения оптимального решения вполне логично выяснить, как отразится на оптимальном решении изменение запасов ресурсов. При этом важно проанализировать два аспекта:

1. На сколько можно увеличить запас некоторого ресурса для улучшения полученного оптимального значения целевой функции.

2. На сколько можно снизить запас некоторого ресурса при сохранении полученного оптимального значения целевой функции.

Поскольку величина запаса каждого из ресурсов фиксируется в правых частях ограничений, то этот вид анализа обычно идентифицируется как анализ модели на чувствительность к правой части (ограничений). Прежде чем ответить на эти вопросы, классифицируем ограничения линейной модели как связывающие (активные) и несвязывающие (пассивные) ограничения. Те прямые (в графическом методе), которые проходят через оптимальную точку, называют связывающими. Они лимитируют запасы исходных ресурсов, и их относят к разряду дефицитных ресурсов, поскольку они используются полностью. Ресурс, с которым ассоциировано несвязывающее ограничение, относят к разряду недефицитных ресурсов, т.е. имеющихся в некотором избытке.

Таким образом, при анализе модели на чувствительность к правым частям ограничений определяются:

- предельно допустимое увеличение запаса дефицитного ресурса, позволяющее улучшить найденное оптимальное решение;

- предельно допустимое снижение запаса недефицитного ресурса, не изменяющее найденного ранее оптимального значения целевой функции.

Информация, полученная в последнем случае, особенно полезна тогда, когда излишки недефицитного ресурса могут быть использованы для других целей. Заметим, что сокращение объёма дефицитного ресурса никогда не улучшает значение целевой функции.

Вторая задача анализа на чувствительность позволяет ответить на вопрос: увеличение объема какого из ресурсов наиболее выгодно? Для решения этой задачи следует ввести характеристику ценности каждой дополнительной единицы дефицитного ресурса, выражаемой через соответствующее приращение оптимального значения целевой функции. Обозначим ценность дополнительной единицы ресурса i через y_i. Величина y_i может быть определена из отношения: