Постановка задачи: 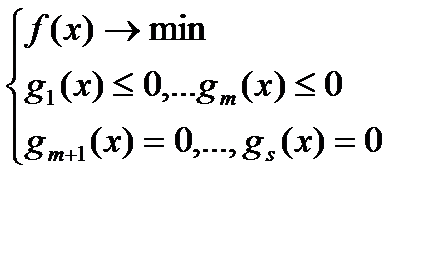 (1), где
(1), где 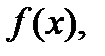
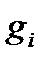 :
: 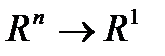 , i = 1
, i = 1 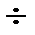 s.
s.
Положим 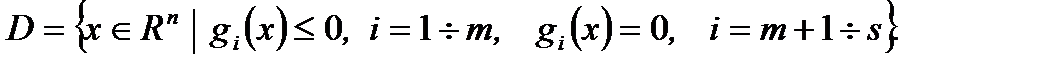
Опр.1 Функция 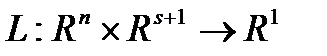 вида
вида 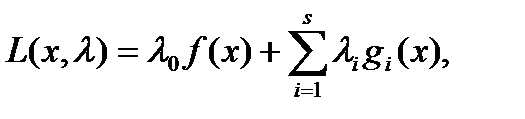
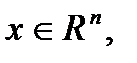
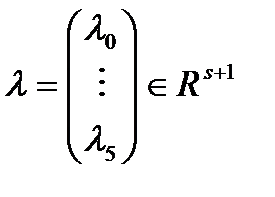 называют функцией Лагранжа для (1).
называют функцией Лагранжа для (1).
Необходимые условия локального максимума формулируются теоремой:
Теорема 1 (Каруша-Джона): Пусть 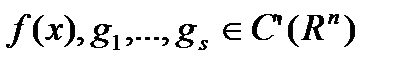 и
и 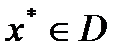 точка локального минимума функции
точка локального минимума функции 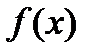 на
на 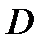 . Тогда существует вектор
. Тогда существует вектор 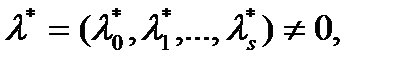 такой что
такой что
1. 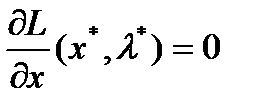 , (условие стационарности);
, (условие стационарности);
2. 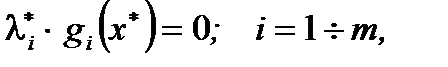 (условие дополняющей нежесткости);
(условие дополняющей нежесткости);
3. 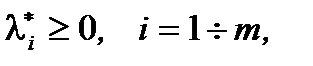 (условие неотрицательности);
(условие неотрицательности);
4. 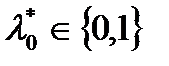 , (условие нормировки).
, (условие нормировки).
С учетом 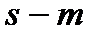 ограничений равенств и условия нормировки количество неизвестных совпадает с количеством равенств в формулировке теоремы 1.
ограничений равенств и условия нормировки количество неизвестных совпадает с количеством равенств в формулировке теоремы 1.
Достаточные условия локального минимума формулируются теоремой:
Теорема 2: Пусть 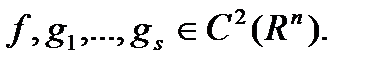 Пара
Пара 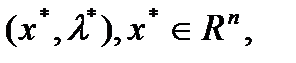
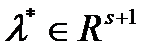 такова, что
такова, что
1. 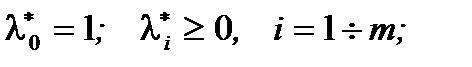
2. 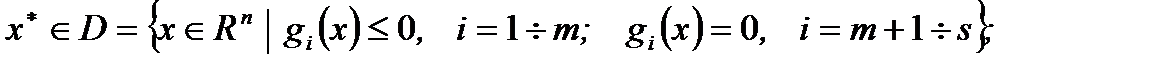
3. 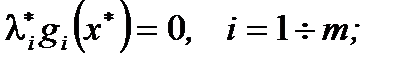
4. 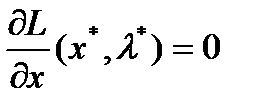 .
.
5. 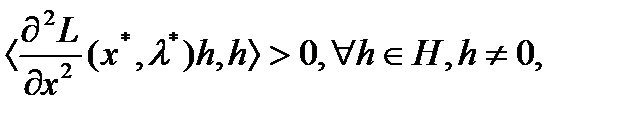 где
где
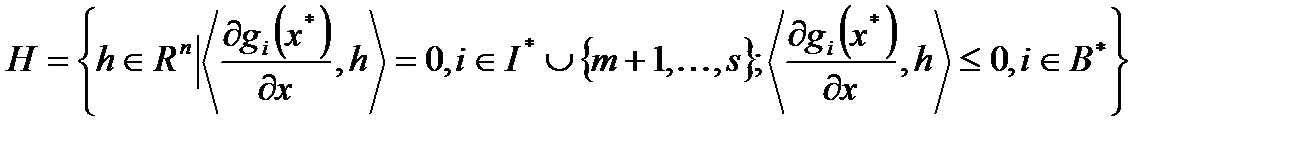 , а
, а 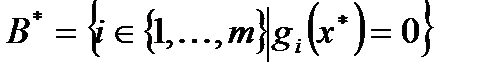 ,
, 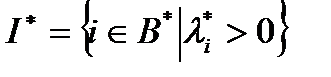 .
.
Тогда 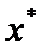 является точкой локального минимума функции
является точкой локального минимума функции 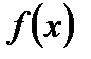 на множестве
на множестве 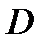 .
.
Замечание. Всякое равенство 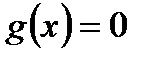 эквивалентно двум неравенствам
эквивалентно двум неравенствам 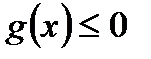 и
и 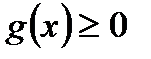 , а всякое неравенство
, а всякое неравенство 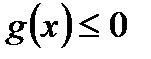 эквивалентно равенству
эквивалентно равенству 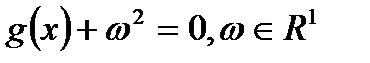 . Это позволяет свести задачу (1) к задаче с ограничениями типа неравенств:
. Это позволяет свести задачу (1) к задаче с ограничениями типа неравенств:
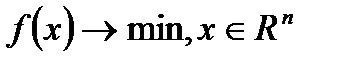 ,
, 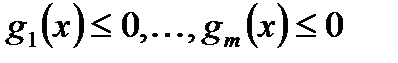 ,
, 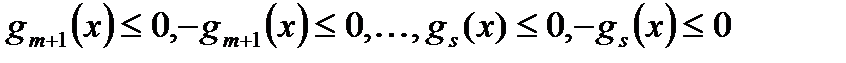 (2)
(2)
либо к задаче с ограничениями равенствами: 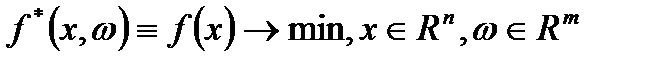 ,
, 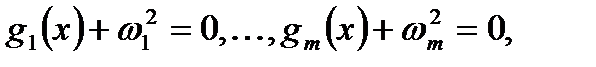
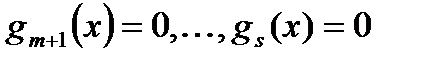 (3)
(3)
Условия локального минимума в случае ограничений равенств (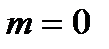 ) принимают вид:
) принимают вид:
Теорема 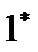 : пусть
: пусть 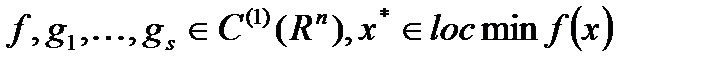 на
на 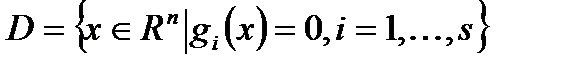 . Тогда
. Тогда 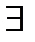 вектор
вектор 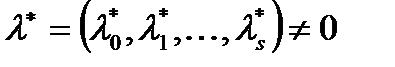 , что
, что 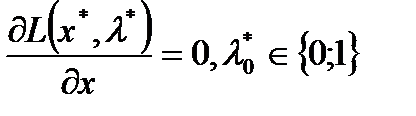 .
.
Теорема 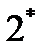 : Пусть
: Пусть 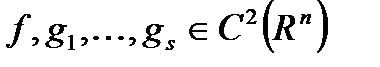 . Пара
. Пара 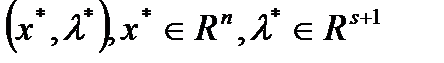 удовлетворяет условиям:
удовлетворяет условиям:
1. 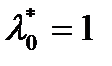 ; 2.
; 2. 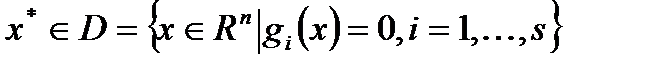 ;
;
3. 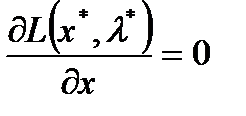 ; 4.
; 4. 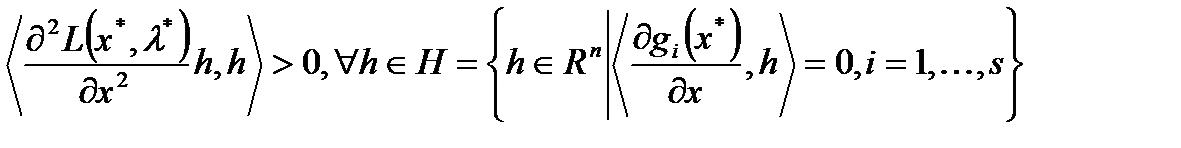 ,
, 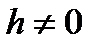 .
.
Тогда 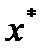 - точка локального минимума
- точка локального минимума 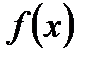 на
на 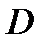 .
.
Опр.2: Локальный минимум для задачи с ограничениями типа равенств (точка 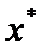 ) называется регулярным, если набор векторов
) называется регулярным, если набор векторов 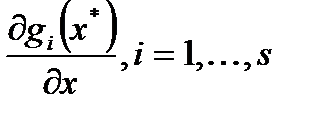 линейно независим.
линейно независим.
Теорема 3: Пусть 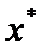 - точка регулярного локального минимума. Тогда в теореме
- точка регулярного локального минимума. Тогда в теореме 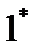 в условиях нормировки можно сразу положить
в условиях нормировки можно сразу положить 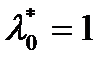 .
.
Док-во:
Пусть 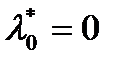 . Тогда справедливо равенство
. Тогда справедливо равенство 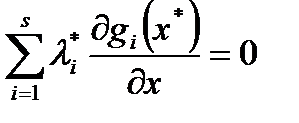 . Т.к. вектор
. Т.к. вектор 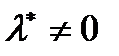 , то не все
, то не все 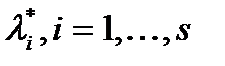 равны 0. Это противоречит линейной независимости векторов
равны 0. Это противоречит линейной независимости векторов 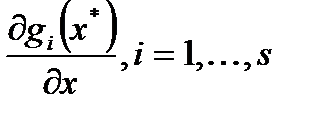 . Таким образом
. Таким образом 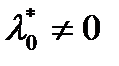 и
и 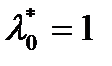 . ч.т.д.
. ч.т.д.
 2015-01-21
2015-01-21 1064
1064








