Опр. 1: Множества 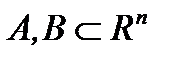 отделимы, если существует вектор
отделимы, если существует вектор 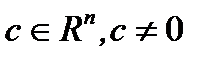 , что
, что 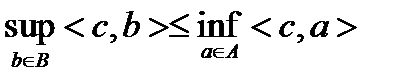 (1) строго отделимы, если
(1) строго отделимы, если 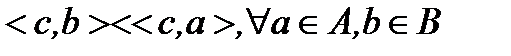 и сильно отделимы, если в (1) знак неравенства строгий.
и сильно отделимы, если в (1) знак неравенства строгий.
Замечание: Геометрический смысл О.1 в существовании гиперплоскости, что А и В лежат в разных полупространствах по отношению к ней. Гиперплоскость отделяющая (строго, сильно).
Теорема 1: Пусть 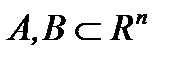 непустые, выпуклые и
непустые, выпуклые и 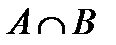 =
=  . Тогда существует гиперплоскость
. Тогда существует гиперплоскость 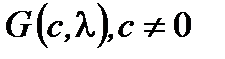 , отделяющая
, отделяющая 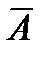 и
и 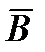 . Если
. Если 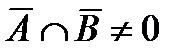 и
и 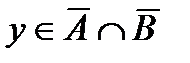 , то
, то 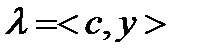
Доказательство: Пусть 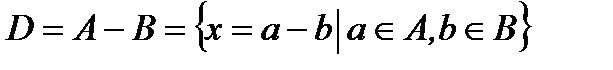 .
. 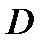 выпукло (Т.2, П.2.1).
выпукло (Т.2, П.2.1). 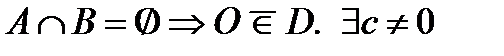 .
. 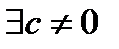 , что
, что 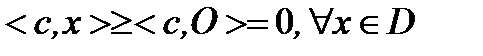 (Т.3, П.2.3). Тогда
(Т.3, П.2.3). Тогда 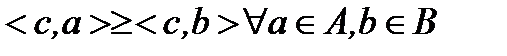 (2)
(2)
Пусть 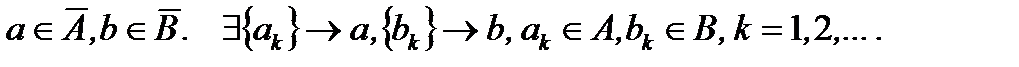 .
.
Из (2) 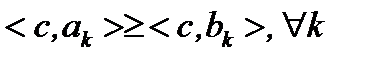 , и при
, и при 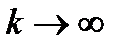
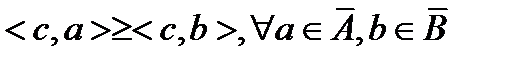 (3) что означает выполнение (1). Пусть
(3) что означает выполнение (1). Пусть 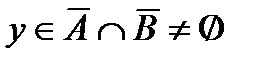 . Тогда из
. Тогда из 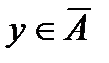 и (3) следует, что
и (3) следует, что 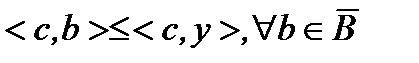 , а из
, а из 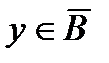 и (3) следует, что
и (3) следует, что 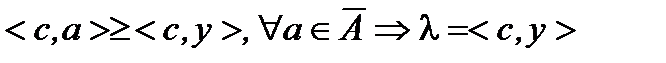 ч.т.д.
ч.т.д.
Теорема 2. Пусть A,B 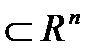 ; A,B
; A,B 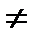
 ,выпуклые замкнутые, одно из них ограничено и A
,выпуклые замкнутые, одно из них ограничено и A  B=
B=  . Тогда A и B строго отделимы. Если они оба ограничены, то отделимость будет сильной.
. Тогда A и B строго отделимы. Если они оба ограничены, то отделимость будет сильной.
Пусть заданы матрица B размерности s 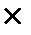 n и вектор
n и вектор 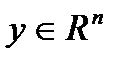 , причем
, причем 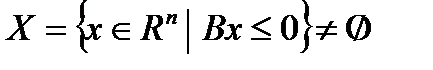 .
.
Теорема 3 (Фаркаша). Неравенство <y,x> 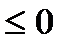 выполняется
выполняется 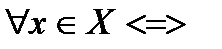 ,если
,если 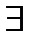
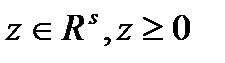 , что
, что 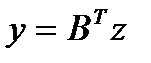 .
.
Доказательство:
Необходимость. Пусть 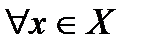 <y,x>
<y,x> 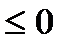 . Докажем, что
. Докажем, что 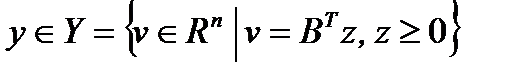 . Пусть
. Пусть 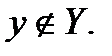 Y- замкнуто и выпукло (замкнутость следует из непрерывности линейных функций). По Т.2
Y- замкнуто и выпукло (замкнутость следует из непрерывности линейных функций). По Т.2 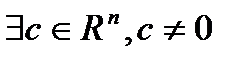 , что
, что

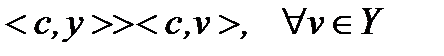 (4)
(4)
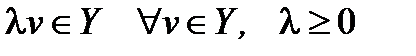 . Из (4) =>
. Из (4) => 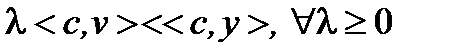 ,
, 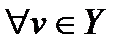 и
и 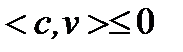 . Но
. Но 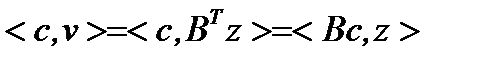
Значит 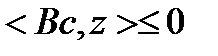
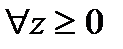 и
и
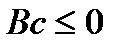 (5)
(5)
Т.к. 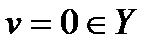 , то
, то
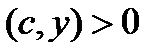 (6)
(6)
Положив 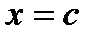 из (5) и (6) получаем противоречие условиям теорем.
из (5) и (6) получаем противоречие условиям теорем.
Достаточность. Пусть 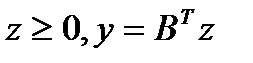 . Тогда
. Тогда 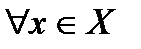
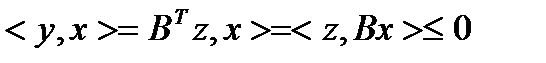 . ч.т.д.
. ч.т.д.
 2015-01-21
2015-01-21 1312
1312








