Свойства выпуклых множеств

Опр. 1. Множество 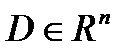называется выпуклым, есл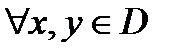и и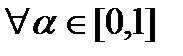

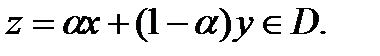
Теорема1. Пересечение любого количества выпуклых множеств выпукло.

Доказательство:

Пусть 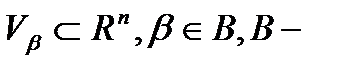множество индексов, 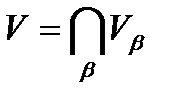. 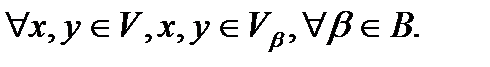А т.к. 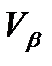выпуклы, то 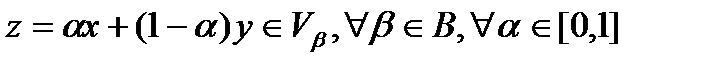и 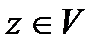, т.е. оно выпукло.

Опр. 2. 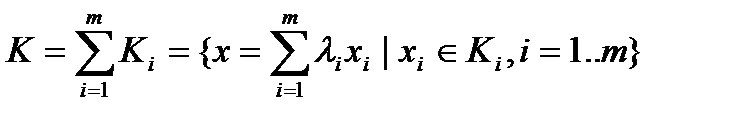, называется алгебраической линейной комбинацией множеств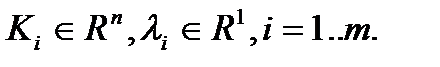

Теорема 2. Любая линейная комбинация конечного числа выпуклых множеств выпукла.

Доказательство:

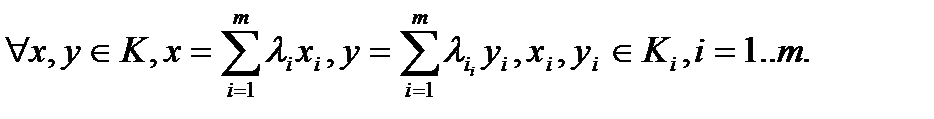
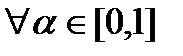
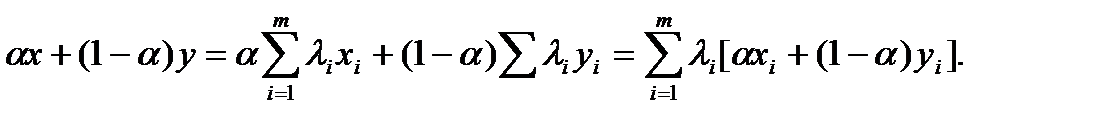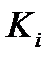Т.к. - выпуклы, то 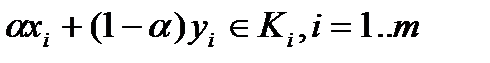и .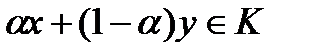

Опр. 3. Точка 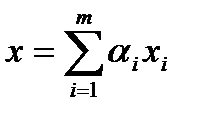, где 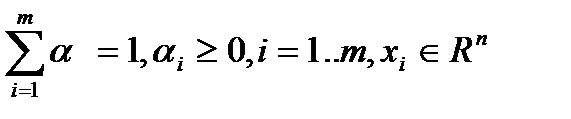называется выпуклой комбинацией точек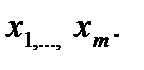

Теорема3. 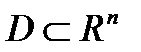выпукло ó D содержит все выпуклые комбинации любого конечного числа своих точек.