Методы оптимизации. Ответы на вопросы.
Постановка задачи: 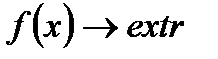 .
.
Опр.1 Пусть 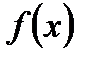 определена на
определена на 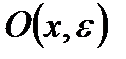 . Она дифференцируема в точке
. Она дифференцируема в точке 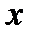 , если
, если 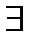 вектор
вектор 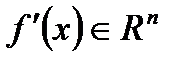 , для которого
, для которого 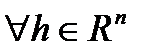 таких, что
таких, что 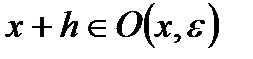 , имеет место равенство:
, имеет место равенство:
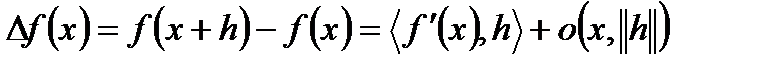 , где
, где 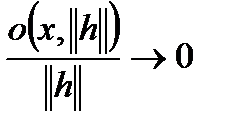 при
при 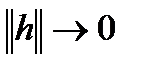 .
.
Обозначения вектора 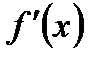 (градиента):
(градиента):
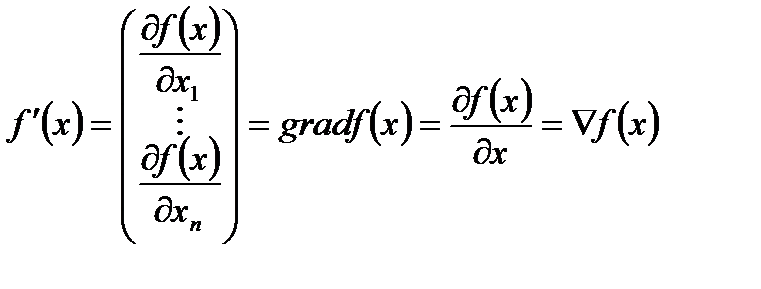
Опр.2: 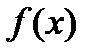 непрерывно дифференцируема на множестве (3) D, если она определена на D и дифференцируема в каждой точке множества D и
непрерывно дифференцируема на множестве (3) D, если она определена на D и дифференцируема в каждой точке множества D и 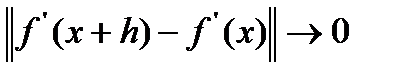 при
при 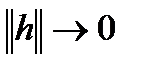
Опр.3: 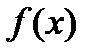 , определенная на
, определенная на 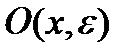 , дважды непрерывно дифференцируема в точке х, если наряду с
, дважды непрерывно дифференцируема в точке х, если наряду с 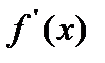 существует симметрическая матрица
существует симметрическая матрица 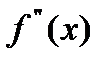 размерности nxn, что
размерности nxn, что 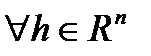 таких, что
таких, что 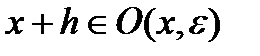 имеет место
имеет место 

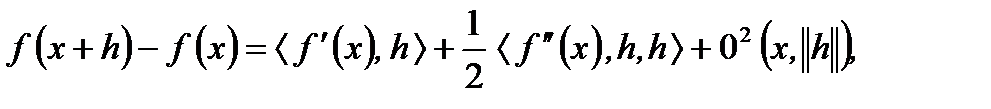 , где
, где 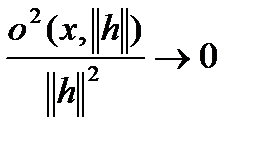 при
при 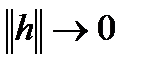 ,
, 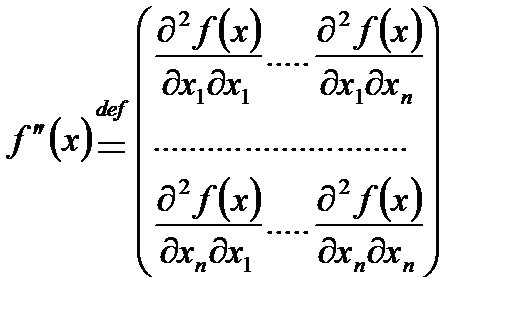
Опр.4: Если 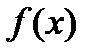 определена на D и дважды дифференцируема в
определена на D и дважды дифференцируема в 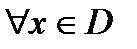 и
и 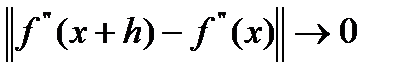 при
при 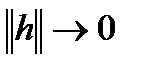 , то
, то 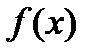 дважды непрерывно дифференцируема.
дважды непрерывно дифференцируема.
Обозначения: 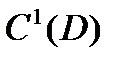 - множество непрерывно дифференцируемых функций,
- множество непрерывно дифференцируемых функций, 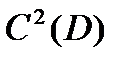 - множество дважды непрерывно дифференцируемых функций на D.
- множество дважды непрерывно дифференцируемых функций на D.
Необходимые условия локального минимума дифференцируемой функции:
Теорема 1: (Ферма) Пусть 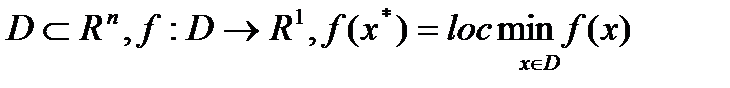 , существует окрестность точки
, существует окрестность точки 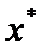 , целиком содержащаяся в множестве D, и
, целиком содержащаяся в множестве D, и 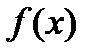 дифференцируема в точке
дифференцируема в точке 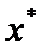 . Тогда
. Тогда 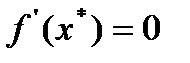 .
.
Док-во:
Из определения locmin следует существование окрестности 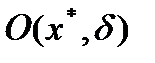 , что
, что 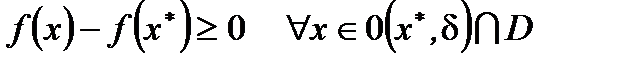 . Из условия теоремы
. Из условия теоремы  , что для всех
, что для всех 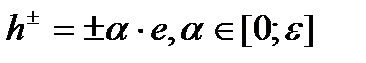 будет справедливо
будет справедливо 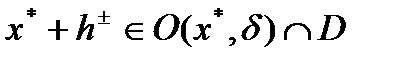 . Из этого включения и условия
. Из этого включения и условия 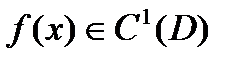 вытекает
вытекает 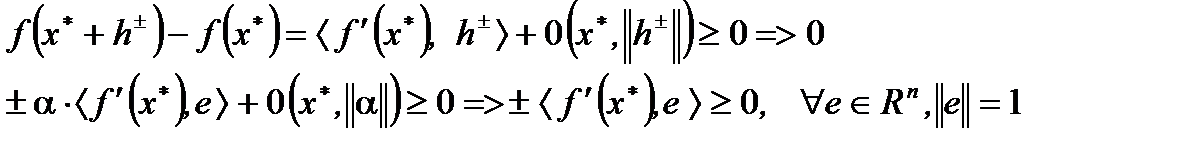
Тогда 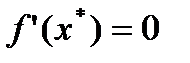 , что эквивалентно условиям
, что эквивалентно условиям 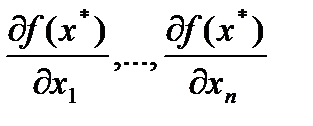
 2015-01-21
2015-01-21 878
878







