Из ограниченности D 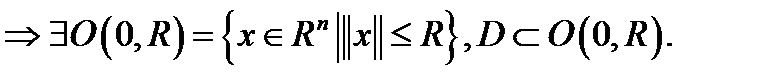 А т.к.
А т.к. 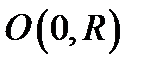 - выпукло
- выпукло 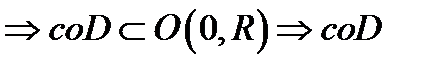 ограниченно. Пусть y – предельная точка
ограниченно. Пусть y – предельная точка 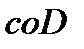 и
и 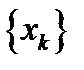 такое, что
такое, что 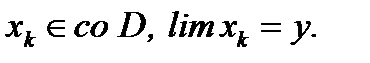 . По Т.2, п.2.2
. По Т.2, п.2.2 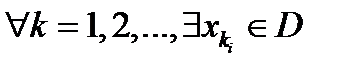 и
и 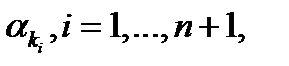 что
что 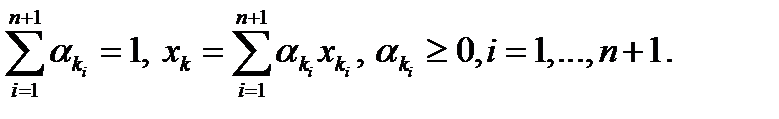 Из ограниченности
Из ограниченности 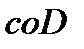 следует существование подпоследовательностей
следует существование подпоследовательностей 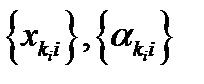 из последовательностей
из последовательностей 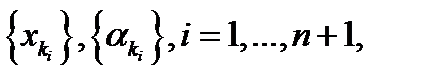 что
что 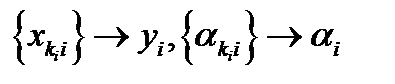 и из замкнутости D
и из замкнутости D 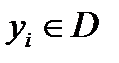 . Перейдя к пределу при
. Перейдя к пределу при 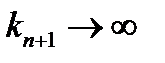 в соотношениях
в соотношениях 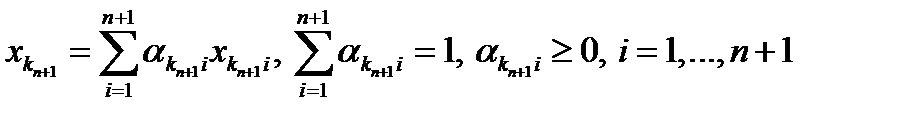 получаем
получаем 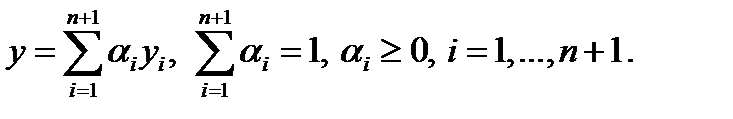
5. Проекция точки на множество.
Опр. 1. Проекцией точки 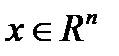 на множество
на множество 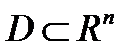 называется точка
называется точка 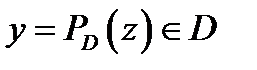 , что
, что 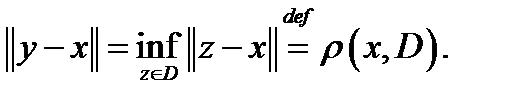
Теорема 1. Для  замкнутого множества
замкнутого множества 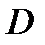 и
и 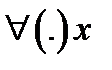 существует ее проекция на
существует ее проекция на 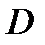 . Если
. Если 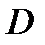 выпукло, то проекция единственна.
выпукло, то проекция единственна.
Теорема 2. Для того, чтобы 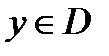 была проекцией x на выпуклое замкнутое множество
была проекцией x на выпуклое замкнутое множество 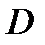
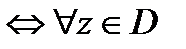 выполнялось
выполнялось 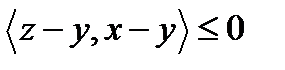 .
.
Теорема 3: Пусть 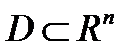 - выпуклое множество. Тогда
- выпуклое множество. Тогда 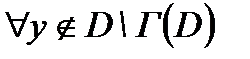 существует вектор
существует вектор 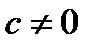 , что
, что 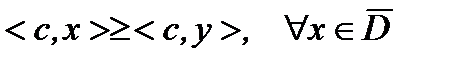 , причем, если
, причем, если 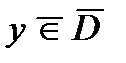 , то
, то 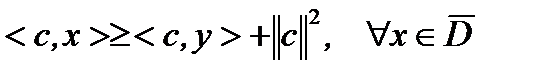 .
.
Замечание: Г 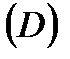 - совокупность всех граничных точек множества
- совокупность всех граничных точек множества 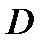 . Геометрический смысл теоремы 3: через любую точку
. Геометрический смысл теоремы 3: через любую точку 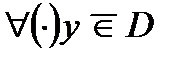 (выпуклому множеству) можно провести гиперплоскость, причем
(выпуклому множеству) можно провести гиперплоскость, причем 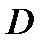 будет располагаться в одном из отвечающих ей полупространств. Если
будет располагаться в одном из отвечающих ей полупространств. Если 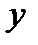 принадлежит границе
принадлежит границе 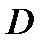 , то гиперплоскость называется опорной, а ее нормальный вектор – опорным вектором к множеству
, то гиперплоскость называется опорной, а ее нормальный вектор – опорным вектором к множеству 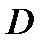 в точке
в точке 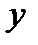 .
.
 2015-01-21
2015-01-21 1115
1115








