2015-01-21
531
Из Т.1.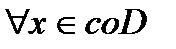 
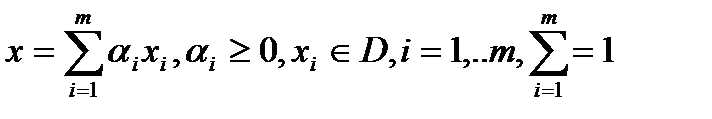(1). Если 
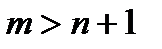, то число ненулевых слагаемых можно уменьшить. Рассмотрим в 
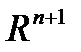векторы 
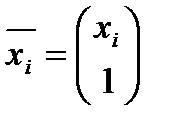i=1..m. Они линейно зависимы, т.к. m>n+1. 
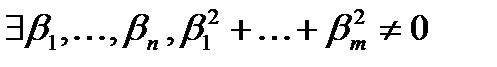,что 
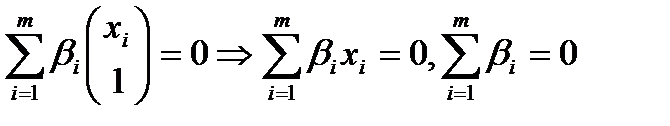(2)
Из (1), (2)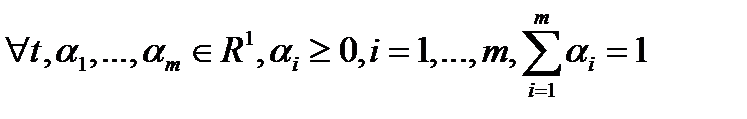 
справедливо 
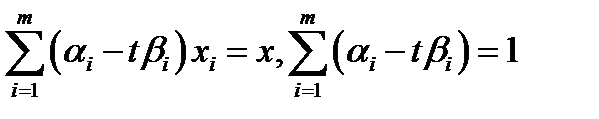, а т.к. не все 
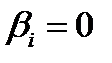, а их сумма равна 0, то среди них есть строго положительные. Пусть 
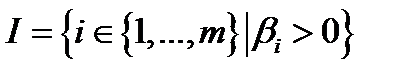, и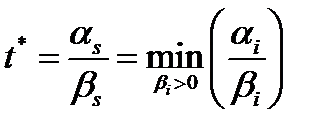 
. Тогда 
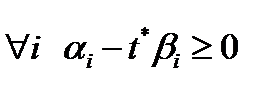и точка x представляется в виде выпуклой комбинации меньшего, чем m числа точек из D.
Теорема 3. Замыкание и внутренность выпуклых множеств выпуклы.
Теорема 4. Если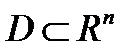 
компактно, то и 
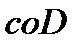компактно.
