2015-01-21
396
Из (Т.1) 
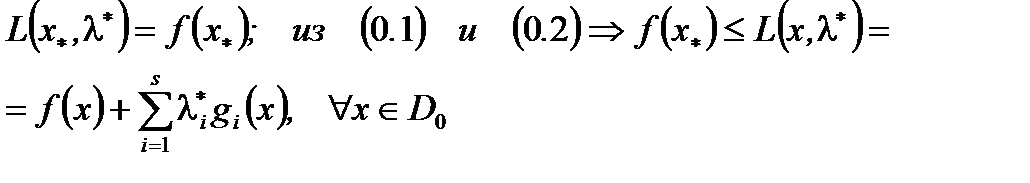(3)
(3) верно и для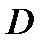 
. Тогда 
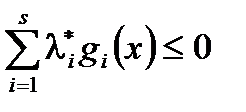и из (3) следует 
.
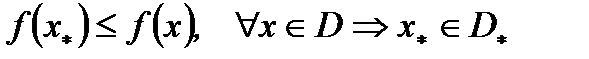11. Теорема Куна-Таккера.
Дополнительные условия, сформулированные Куном-Таккером в различных по постановкам теоремам являются обобщением принципа Лагранжа. Рассмотрим случай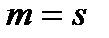 
задачи ВП. Тогда 
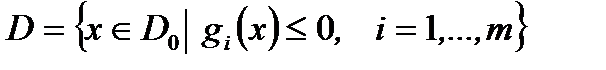. (1)
Опр. 1. Множество (1) называется регулярным (выполнение условия Слейтера), если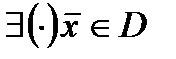 
такая, что 
.
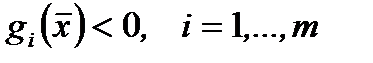Замечание. Для выполнения условия Слейтера достаточно потребовать: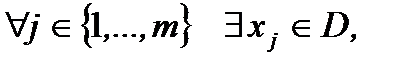 
что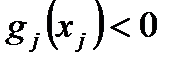 
. Тогда из выпуклости 
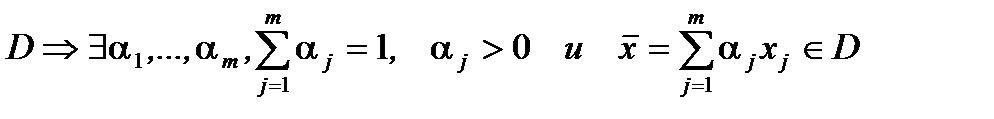, а из выпуклости 
.
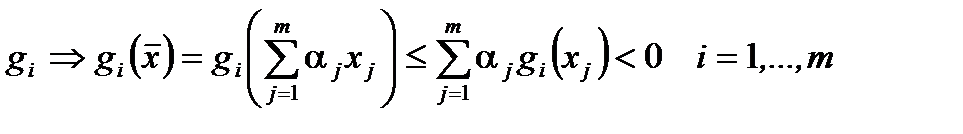Теорема 1 (Куна-Таккера). Пусть в задаче ВП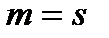 
, выполнено условие регулярности и 
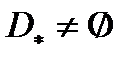. Тогда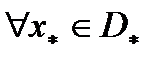 
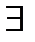вектор 
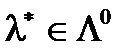такой, что 
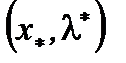является седловой точкой функции Лагранжа для этой задачи.
