2015-01-21
333
Необходимость. Пусть выполнено (1). Покажем, что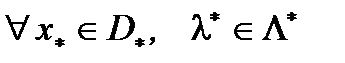 
пара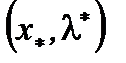 
является седловой для функции Лагранжа имеем 
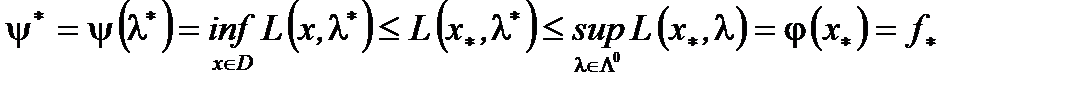(2)
Т.к.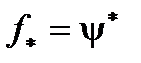 
из (2) следует 
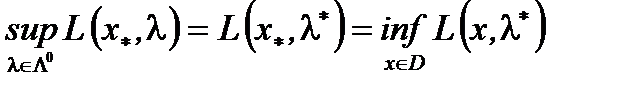(3). Последнее равенство означает, что 
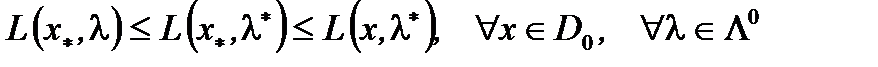.Таким образом, пара 
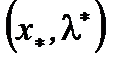- седловая точка и множество 
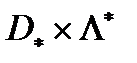принадлежит множеству точек функции Лагранжа.
Достаточность. Пусть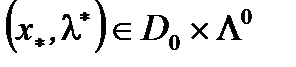 
- седловая точка функции Лагранжа. Тогда
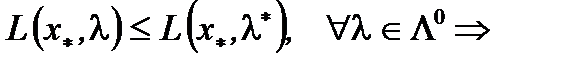
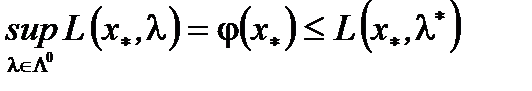(4). Аналогично, из неравенства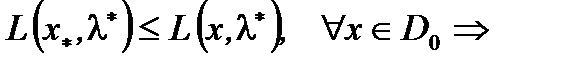 
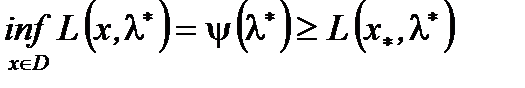(5). Из (3) и (5) с учетом Т.1 получаем 
.
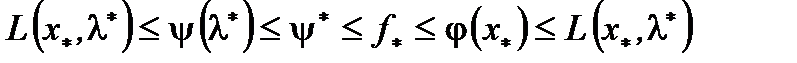Тогда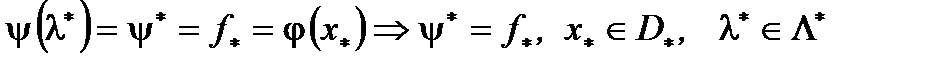 
.
Отсюда выводим, что множество седловых точек функции Лагранжа принадлежит множеству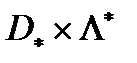 
.
Теоремы 1 и 2 в совокупности образуют теорему двойственности.
Замечание. Если задача линейного программирования имеет решение, то для нее существует седловая точка функции Лагранжа. Тогда по Т.2 двойственная задача имеет решение и значения целевых функций этих точек совпадают.
