2015-01-21
2655
Вектор –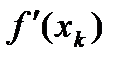 
является направлением наискорейшего убывания функции f(x) и называется антиградиентом. Выбирая в качестве спуска 
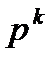антиградиент функции f(x) в точке 
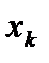, приходим к итерационному процессу вида 
.
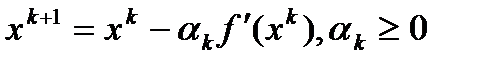Все итерационные процессы, в которых направление движения на каждом шаге совпадает с антиградиентом (градиентом) функции, называется градиентными методами и отличаются друг от друга способами выбора длины шага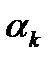 
.Существует много различных способов выбора длины шага 
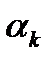, но наиболее распространены три из них. Первый называется методом с постоянным шагом: 
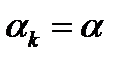. Второй-метод с дроблением шага. Он связан с проверкой на каждом шаге неравенства 
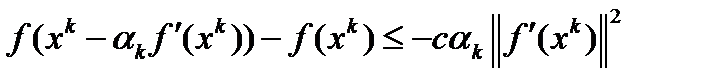, где с - некоторая константа из интервала (0,1). В третьем методе при переходе из точки 
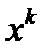в точку 
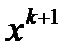минимизируется по 
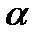функция 
: 
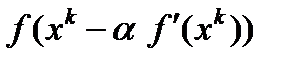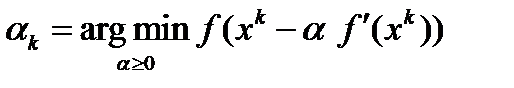. Это метод наискорейшего спуска.
Следующая теорема содержит достаточные условия сходимости метода с постоянным шагом.
Теорема 1. (Первая теорема сходимости). Пусть функция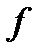 
дифференцируема в 
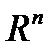, ограничена снизу 
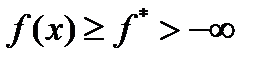, выполняется условие Липшица для градиента 
: 
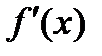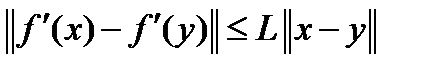и длина шага 
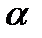удовлетворяет условию 
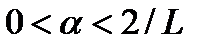. Тогда 
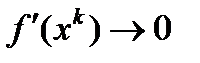при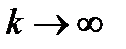 
и при любом выборе начального приближения 
.
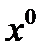Доказательство.
Воспользуемся формулой конечных приращений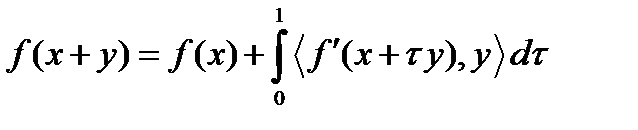 
, которую перепишем в следующем виде: 
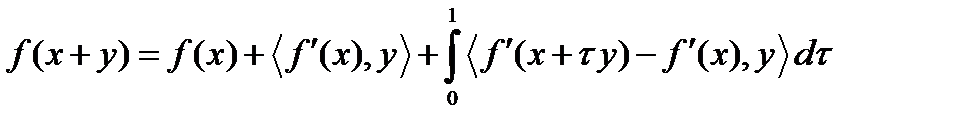. Сделаем подставки 
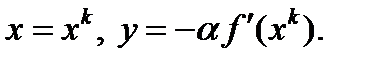Тогда из неравенства Коши-Буняковского 
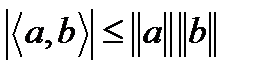и условия Липшица получим
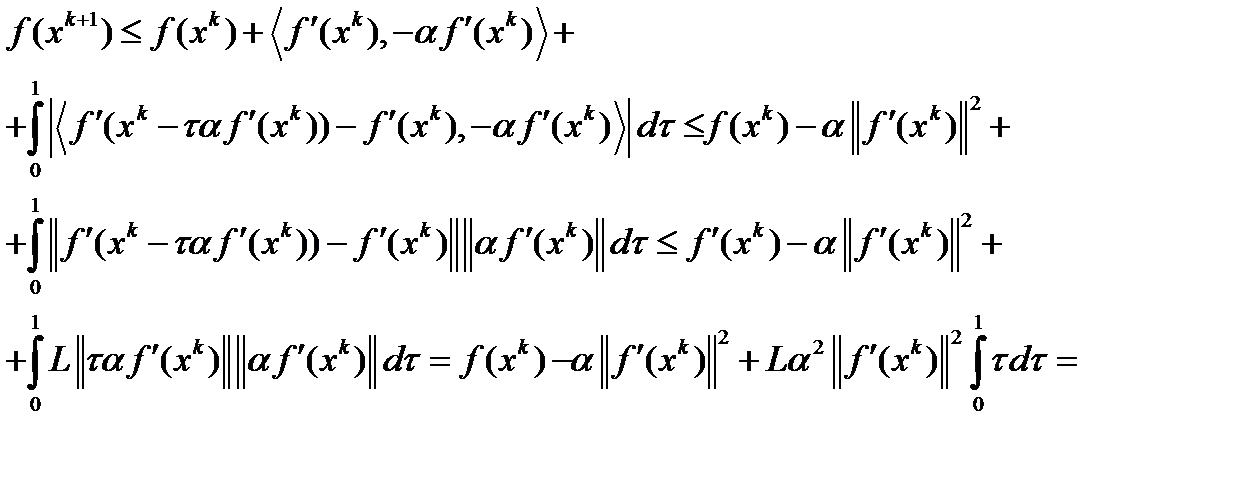
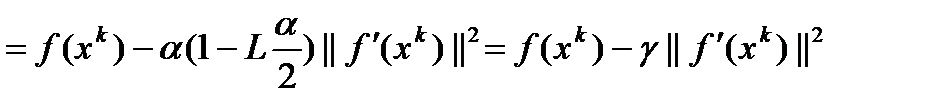, где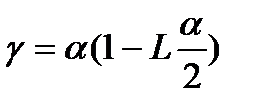 
.
Из условий теоремы следует, что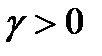 
и, следовательно 
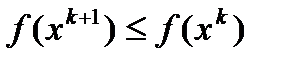. Кроме того, для любого s выполняется неравенство 
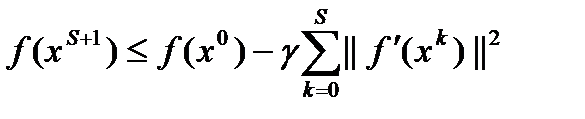. Поэтому, учитывая ограниченность функции 
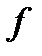на множестве 
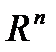, получаем оценку сверху для частичных сумм:
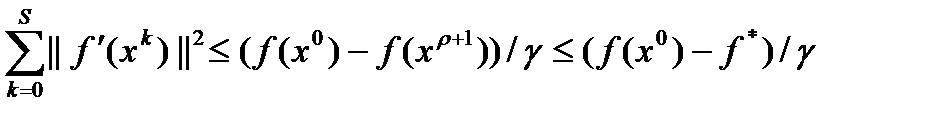. Отсюда и следует сходимость к нулю градиенты 
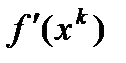при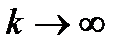 
ч.т.д.
В условиях теоремы 1 градиентный метод обеспечивает сходимость последовательности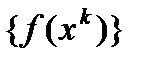 
либо к точной нижней грани 
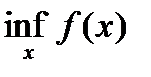(если функция не имеет минимума), либо к значению 
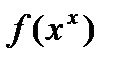, где 
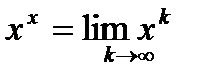и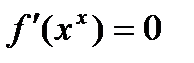 
(если такой предел существует). Существуют примеры, когда в точке 
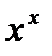реализуется седло, а не минимум. Тем не менее, на практике методы градиентного спуска обычно обходят седловые точки и находят локальные минимумы целевой функции. Для оценки скорости сходимости метода, предположений теоремы 1 недостаточно. Сделаем это в случае, когда 
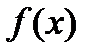сильно выпуклая функция.
Опр.1 Дифференцируемая функция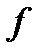 
называется сильно выпуклой (с константой 
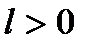), если для любых x и y из 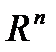справедливо 
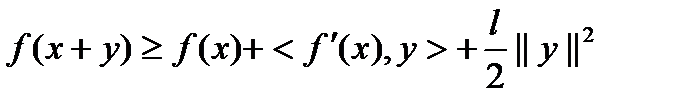(1)
Лемма 1. Если функция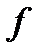 
является сильно выпуклой (с константной 
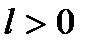), то она имеет глобальный минимум на .
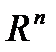Доказательство:
Из условия (1) и неравенства Коши-Бублековского следует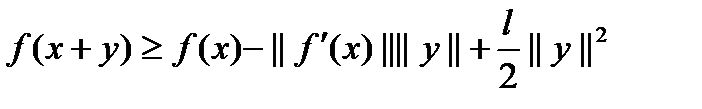 
. Пусть 
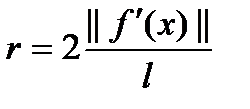. Если 
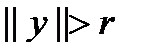, то 
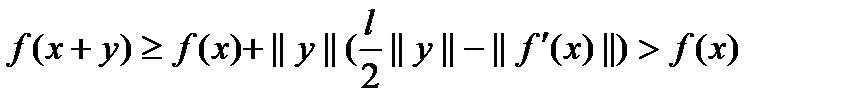(2).
Рассмотрим шар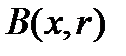 
с центром в точке x и радиуса r. По теореме Вейерштрасса непрерывная функция достигает своего минимума на шаре 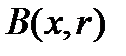в некоторой точке 
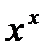. Из неравенства (2) следует, что 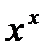минимума на всем 
.
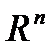Лемма2. Если функция f является сильно выпуклой (с константой l >0) и x* - ее глобальный минимум, то для любого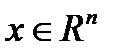 
выполняется неравенство 
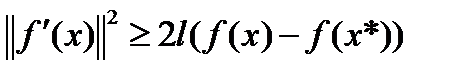(3)
Доказательство. 
Т.к. функция f сильно выпуклая, то подстановка y=x*-xb (1) дает следующее неравенство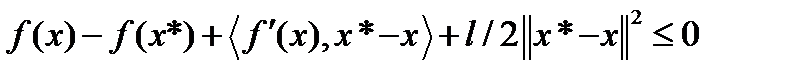 
Т.к. 
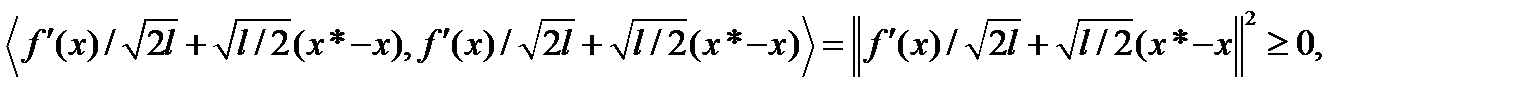то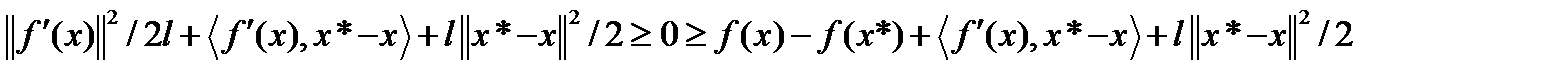 
После приведение подобных членов получим требуемое неравенство.
Теорема2(Вторая теорема сходимости) Пусть функция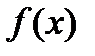 
дифференцируема в 
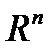, является сильно выпуклой, выполняется условие Липшица для градиента 
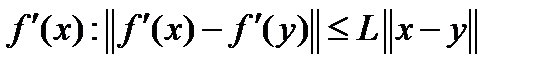и длина шара 
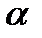удовлетворяет условию 
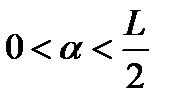. Тогда 
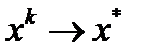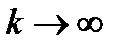при 
и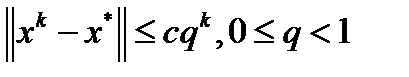 
Доказательство:
Воспользуемся неравенством, полученным при доказательстве теоремы 1: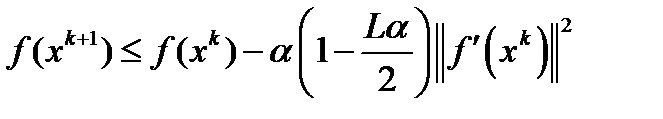 
. По лемме1 существует глобальный минимум 
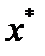функции 
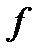. Используя (3), получим 
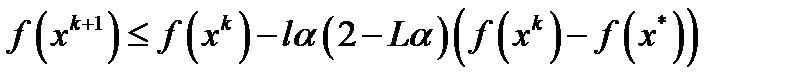(4).Обозначим через 
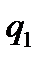коэффициент при выражении 
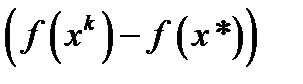. Понятно, что 
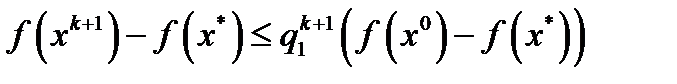(5).Проверим, что 
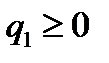. Функция 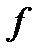является сильно выпуклой. Значит она не может быть константой и имеется возможность выбрать начальную точку 
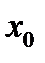так, чтобы 
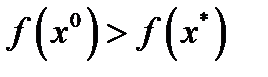. Из неравенства (4) при 
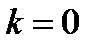имеем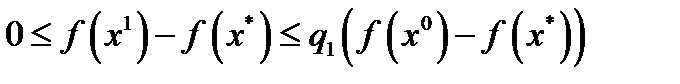 
, откуда и следует требуемое неравенство. Т.к. 
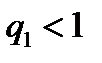, то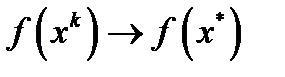 
. Учитывая, что 
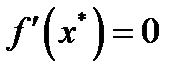, из (1) при подстановках 
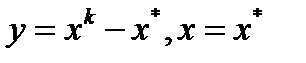получим 
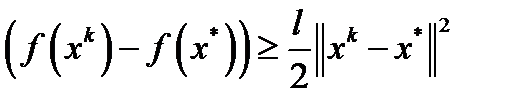. Следовательно, 
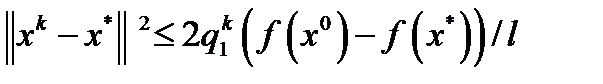. Последнее неравенство влечет линейную оценку скорости сходимости метода 
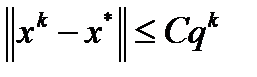, где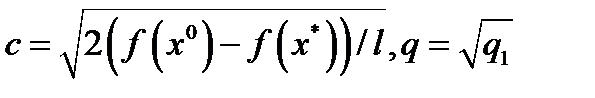 
, а также сходимость последовательности 
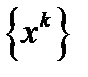к единственной точки минимума 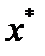. ч.т.д.
