Критерии выпуклости функций

Рассмотрим гладкие функции.

Теорема 1(Первый критерий): 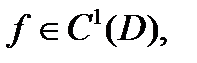где выпукло, является выпуклой функцией .

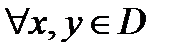Доказательство:

Необходимость: - выпукла на 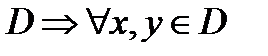и

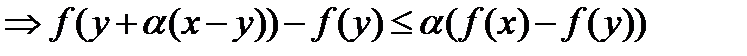и применяя формулу к последнему неравенству имеем Разделив его на и устремив получаем .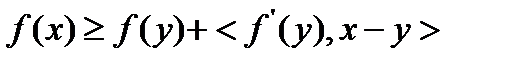

Достаточность: Пусть Из исходного неравенства Первое умножается на , второе на 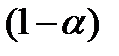и складываем их:

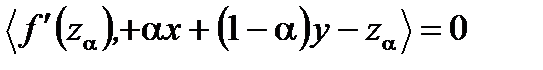
. ч.т.д.

Теорема 2 (Второй критерий) , где 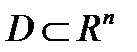выпукло, является выпуклой функцией .

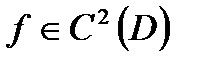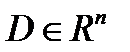Теорема 3 (критерий выпуклости дважды дифференцируемой функции) , где выпукло, является выпуклой функцией, если 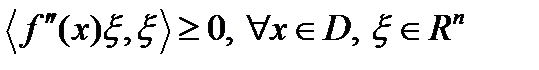, (1)

И если 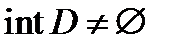, то это условие является необходимым.

Доказательство:

Необходимость: Пусть , , что , если 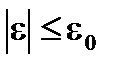. Из Т.2 и формулы следует (2). Сокращая (2) на и 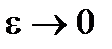получим (1). Если , то т.к. в выпуклом множестве нет изолированных точек 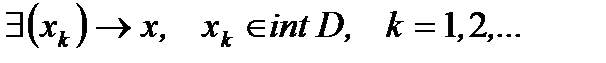и 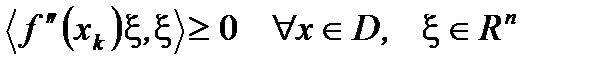. Переходя к получим (1) для .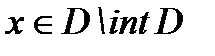

Достаточность. Пусть 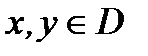и . Из (1) и формулы следует , т.е. для 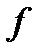выполнены условия Т.2. ч.т.д.