Рассмотрим в 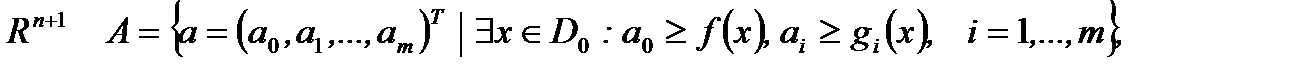
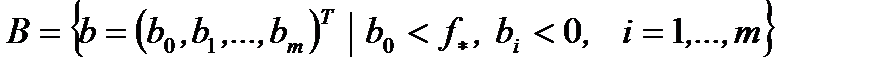 . Покажем:
. Покажем: 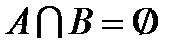 . Пусть
. Пусть 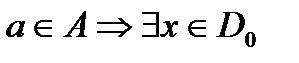 , что
, что 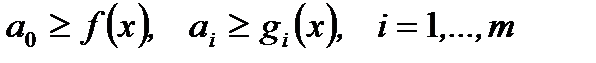 . Если
. Если 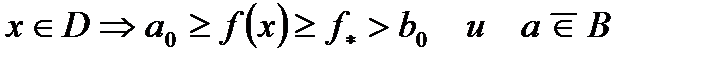 . Если
. Если 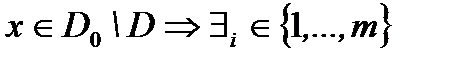 , что
, что 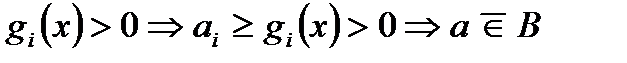 .
.
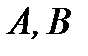 - выпуклы!
- выпуклы! 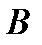 - т.к. оно пересечение конечного числа полупространств. Покажем для
- т.к. оно пересечение конечного числа полупространств. Покажем для 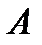 . Пусть
. Пусть 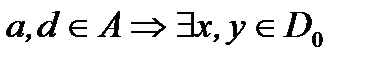 , что
, что 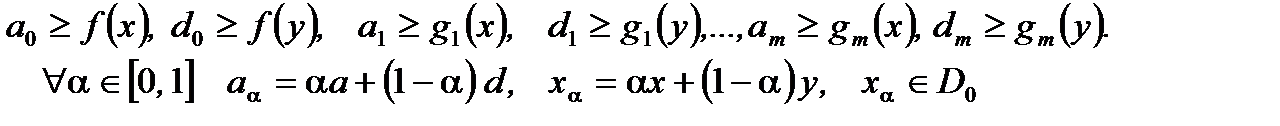
Из выпуклости 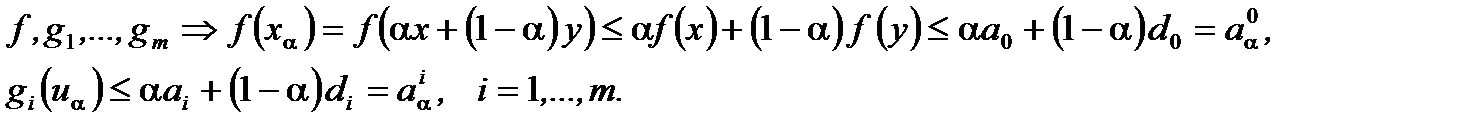
И 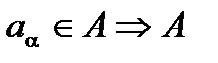 выпукло.
выпукло.
Из (Т.1, п.2.4) 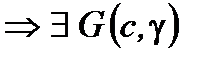 - гиперплоскость,
- гиперплоскость, 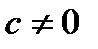 отделяющая
отделяющая 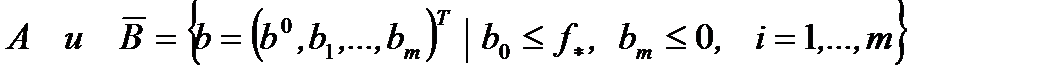 . Обозначим
. Обозначим
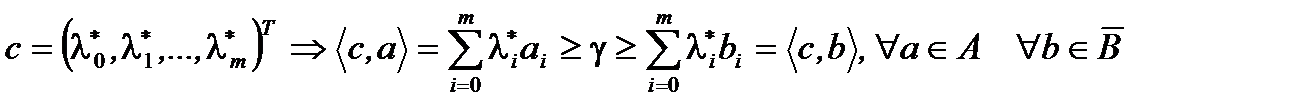 (2) Покажем:
(2) Покажем: 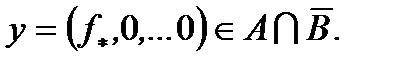 Действительно, пусть
Действительно, пусть 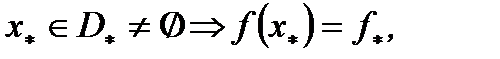
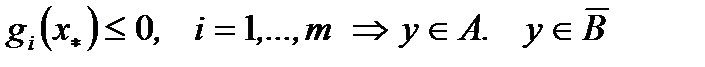 (очевидно)
(очевидно) 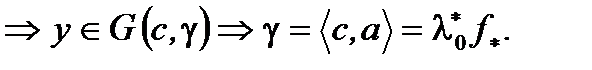 Тогда
Тогда
(2) перепишется: 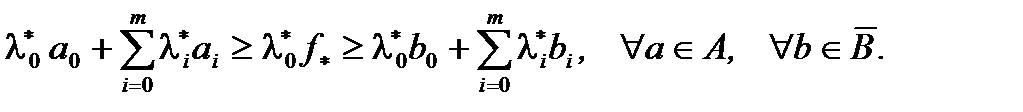 (3)Из (3) выведем:
(3)Из (3) выведем: 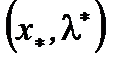 , где
, где 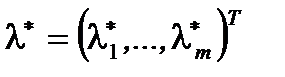 удовлетворяет условиям (Т.4.1.1) и является Седловой точкой.
удовлетворяет условиям (Т.4.1.1) и является Седловой точкой.
Пусть 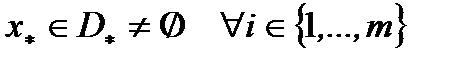 положим
положим 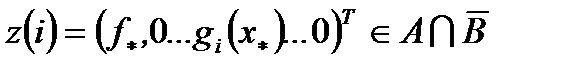 . Из левой части (3) для
. Из левой части (3) для 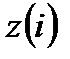 получаем
получаем 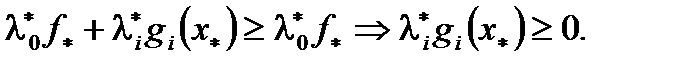 Из правой части (3)
Из правой части (3) 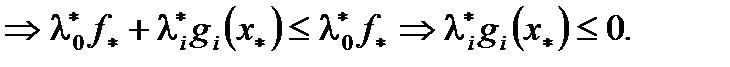 Значит
Значит 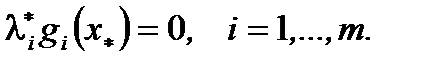 (4)
(4)
В 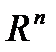 рассмотрим
рассмотрим 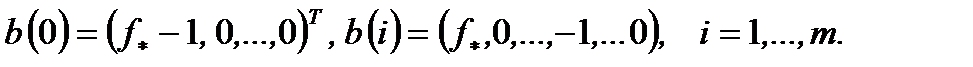
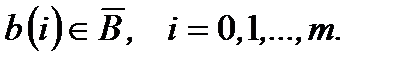 Подставляя
Подставляя 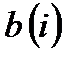 в правую часть (3), получим:
в правую часть (3), получим: 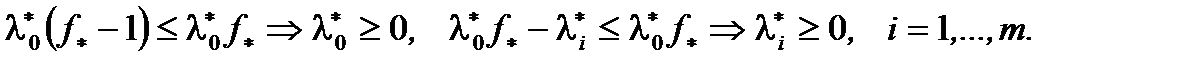 Покажем, что
Покажем, что 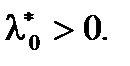 Пусть
Пусть 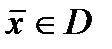 точка, фигурирующая в условиях Слейтера, тогда
точка, фигурирующая в условиях Слейтера, тогда 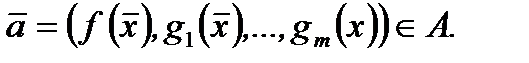 Для
Для 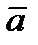 из левой части (3) находим
из левой части (3) находим 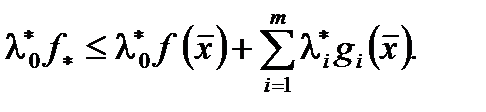 (5)
(5)
Предположим, 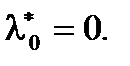 Тогда, т.к.
Тогда, т.к. 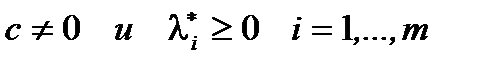 из условий Слейтера следует
из условий Слейтера следует 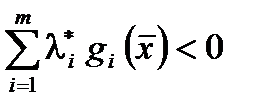 . Это противоречит (5), т.е. значит
. Это противоречит (5), т.е. значит 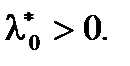 Поделив
Поделив  на
на 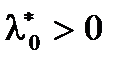 можно считать
можно считать 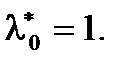 Осталось показать, что
Осталось показать, что 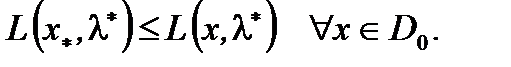 (6)
(6)
Пусть 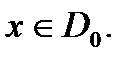 Для
Для 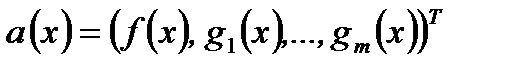 выполняется
выполняется 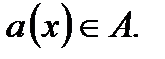 С учетом
С учетом 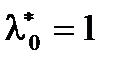 из левой части (3) для этой точки получим
из левой части (3) для этой точки получим 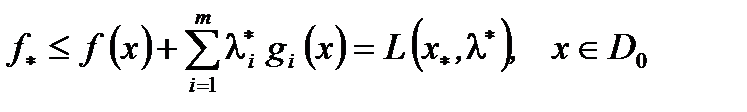 и в силу (4) получаем условие (6).
и в силу (4) получаем условие (6).
Замечание. При 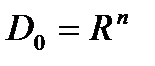 задача ВП является частным случаем задачи 1 (П.3.1). Предположим, что в задаче ВП
задача ВП является частным случаем задачи 1 (П.3.1). Предположим, что в задаче ВП 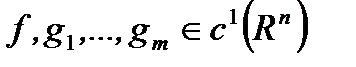 . Тогда условие 1 в (Т.1., п.4.2) принимает вид
. Тогда условие 1 в (Т.1., п.4.2) принимает вид 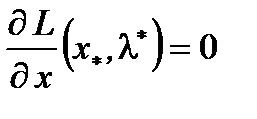 и из теоремы Куна-Таккера вытекает теорема Кароша-Джона, в которой
и из теоремы Куна-Таккера вытекает теорема Кароша-Джона, в которой 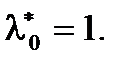 Обратно, если в задаче ВП некоторая точка
Обратно, если в задаче ВП некоторая точка 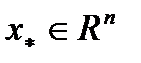 удовлетворяет условиям (Т.1, п.1.3) при
удовлетворяет условиям (Т.1, п.1.3) при 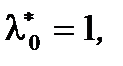 то по Т.,п.4.2 пара
то по Т.,п.4.2 пара 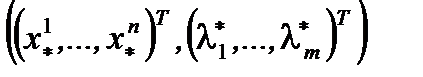 является седловой точкой функции Лагранжа этой задачи и по Т.2, п.4.2 точка
является седловой точкой функции Лагранжа этой задачи и по Т.2, п.4.2 точка 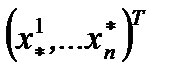 доставляет решение задаче ВП.
доставляет решение задаче ВП.
12. Связь между основной и двойственной задачами.
Пусть 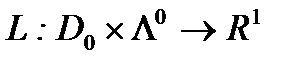 - функция Лагранжа для задачи ВП. Введем в рассмотрение функцию
- функция Лагранжа для задачи ВП. Введем в рассмотрение функцию 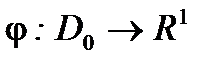 ,
, 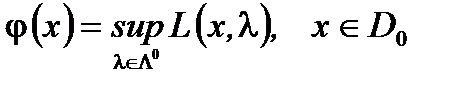
Тогда 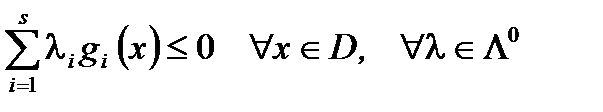 и при
и при 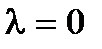 неравенство переходит в равенство. Если
неравенство переходит в равенство. Если 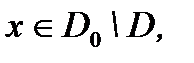 то либо
то либо 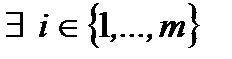 , что
, что 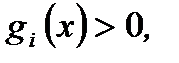 либо
либо 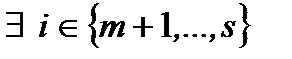 , что
, что 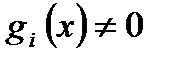 . В любом случае
. В любом случае 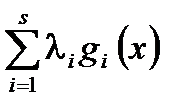 выбором
выбором 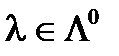 можно сделать сколь угодно большой, поэтому
можно сделать сколь угодно большой, поэтому 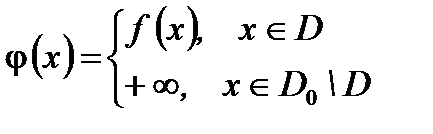 и
и 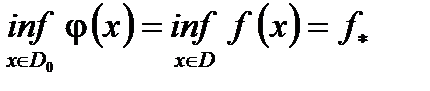 .
.
Поэтому исходная задача может быть записана в виде:
Задача 1. 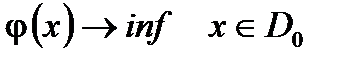 .
.
Поступим аналогичным образом, поменяв роль переменных и операций максимизации и минимизации, т.е. введем наряду с функцией 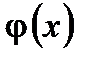 функцию
функцию 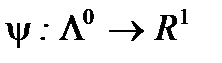 , определенную формулой
, определенную формулой 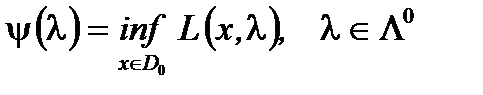 и рассмотрим задачу.
и рассмотрим задачу.
Задача 2. 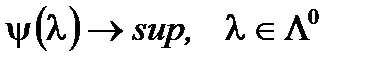 .
.
Опр. 1. Задача 2 называется двойственной к задаче 1, которая называется основной. Переменные 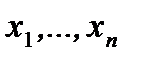 называются основными, а
называются основными, а 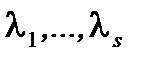 двойственными. В качестве примера рассмотрим следующую задачу:
двойственными. В качестве примера рассмотрим следующую задачу:
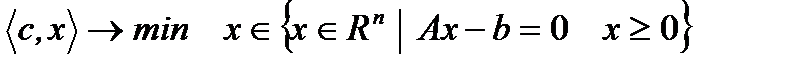 , (1) где А – матрица размерности
, (1) где А – матрица размерности 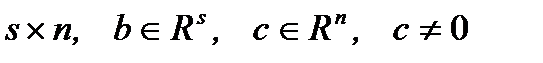 . Она называется задачей линейного программирования в канонической форме. Для этой задачи
. Она называется задачей линейного программирования в канонической форме. Для этой задачи 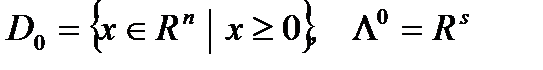 ,а функция Лагранжа
,а функция Лагранжа 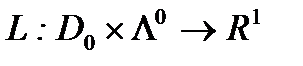 имеет вид:
имеет вид: 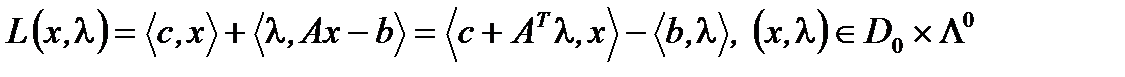 .
.
Функция 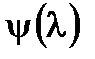 выписывается в явном виде
выписывается в явном виде 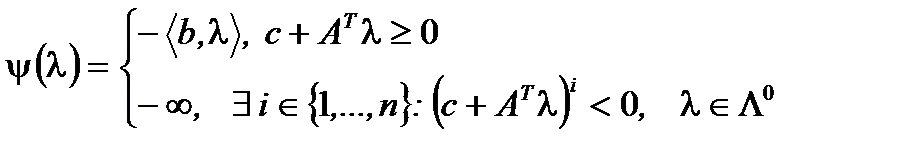
Отсюда ясно, что точку 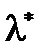 , на которой может достигаться верхняя грань функции
, на которой может достигаться верхняя грань функции 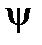 , достаточно искать во множестве
, достаточно искать во множестве 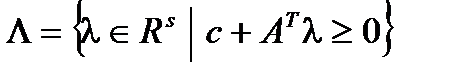 . Двойственная задача к задаче (1) формулируется следующим образом:
. Двойственная задача к задаче (1) формулируется следующим образом: 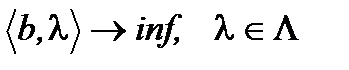 (2). Таким образом, двойственная задача к задаче (1) тоже является задачей линейного программирования. Можно показать, что двойственная задача к задаче (2) будет исходной задачей (1).
(2). Таким образом, двойственная задача к задаче (1) тоже является задачей линейного программирования. Можно показать, что двойственная задача к задаче (2) будет исходной задачей (1).
Замечание. В общем случае задача двойственная к двойственной не всегда совпадает с исходной.
Задачи 1 и 2 из предыдущего пункта тесно связаны между собой. Обозначим 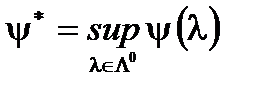 .
.
Теорема 1. Имеет место неравенство 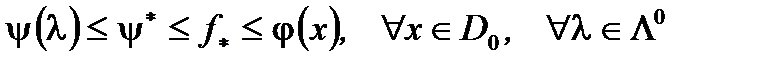 .
.
 2015-01-21
2015-01-21 434
434








