Доказательство. Воспользуемся следующей формулой конечных приращений

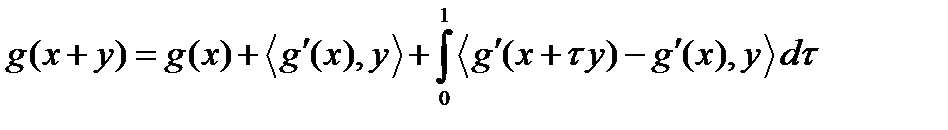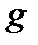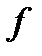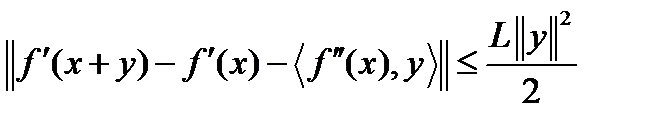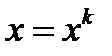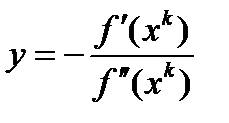Воспользуемся следующей формулой конечных приращений: . Подставим вместо производную функции и, применяя неравенство Коши-Буняковского, получим . Тогда для и имеем 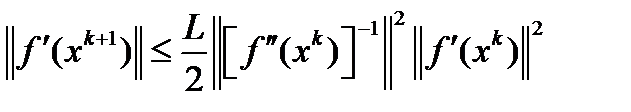. Применяя лемму 1, получим 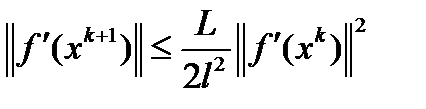. Итерируя это неравенство по 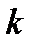, приходим к неравенству 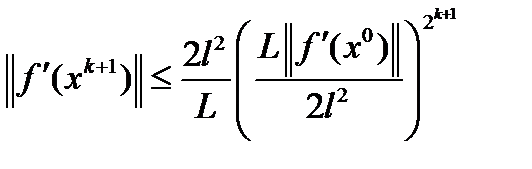, 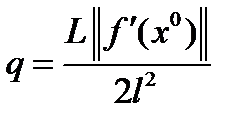. Остается показать, что 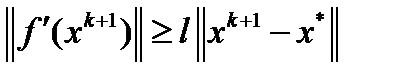. Из определения 1 (п.6.3) сильной выпуклости имеем 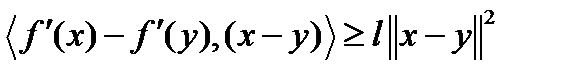. Тогда при подстановке 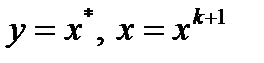, учитывая равенство 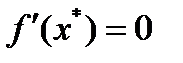, получим 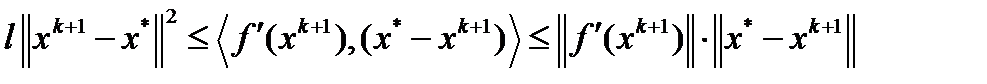, откуда и следует требуемое неравенство.