Перейдем к изложению метода второго порядка, использующего вторые частные производные минимизируемой функции 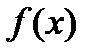 . Этот метод является прямым обобщением метода Ньютона для отыскания решения систем уравнений
. Этот метод является прямым обобщением метода Ньютона для отыскания решения систем уравнений 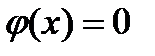 , где
, где 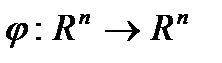 . Возьмем линейную аппроксимацию функции
. Возьмем линейную аппроксимацию функции 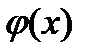 в окрестности точки
в окрестности точки 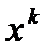 и перепишем уравнение в следующем виде:
и перепишем уравнение в следующем виде: 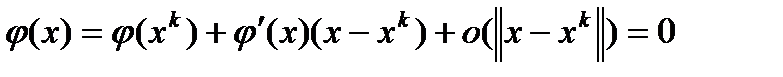
Отбрасывая последний член в этом разложении, получим линейную систему уравнений относительно нового приближения 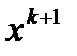 . Таким образом, метод Ньютона отыскания решения системы уравнений описывается следующей формулой:
. Таким образом, метод Ньютона отыскания решения системы уравнений описывается следующей формулой: 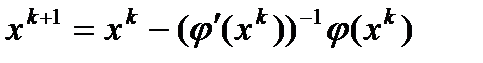
Рассмотрим теперь случай, когда 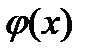 является градиентом некоторой функции
является градиентом некоторой функции 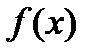 . Формула метода Ньютона для решения уравнения
. Формула метода Ньютона для решения уравнения 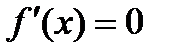 выглядит так:
выглядит так: 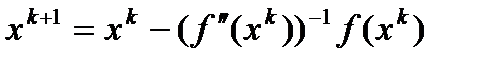
В этом случае метод Ньютона может интерпритировать как поиск точки минимума квадратичной аппроксимации функции 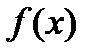 в окрестности точки
в окрестности точки 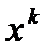 .
.
Лемма1. Пусть 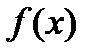 дважды непрерывно дифференцируемая функция. Если
дважды непрерывно дифференцируемая функция. Если 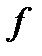 -сильно выпуклая функция с константой
-сильно выпуклая функция с константой 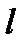 , то выполняется следующее неравенство:
, то выполняется следующее неравенство: 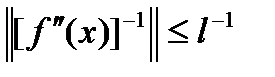
 2015-01-21
2015-01-21 500
500








