НА ТЕМУ «ИЗГИБ С КРУЧЕНИЕМ»

Для стального вала постоянного поперечного сечения с двумя зубчатыми колесами (рис. 5.1,а), передающего мощность Р = 15 кВт при угловой скорости 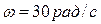, определить диаметр вала по двум вариантам: а) используя третью гипотезу прочности; б) исполь­зуя пятую гипотезу прочности. Принять: ; ; .

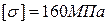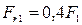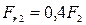Решение:

1. Составляем расчетную схему вала, приводя дейст­вующие на вал нагрузки к оси (рис. 5.1, б). При равномерном вращении вала М₁ = М₂, где М₁ и М₂ - скручивающие пары, которые добавля­ются при переносе сил F₁ и F₂ на ось вала.

2. Определяем вращающий момент, действующий на вал:

.

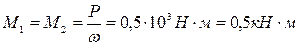3. Вычислим нагрузки, приложенные к валу:

; ;

; .

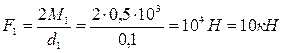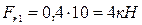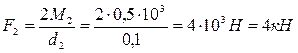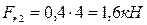4. Определяем реакции опор в вертикальной плоскости (рис. 5.1, б):

;

;

;

;

.

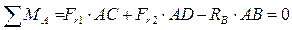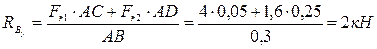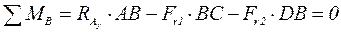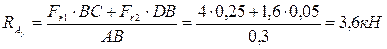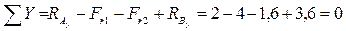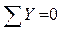, следовательно, 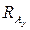, и 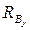найдены правильно.

Определяем реакции опор в горизонтальной плоскости (рис. 5.1, б):

.

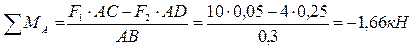Знак минус указывает, на то, что истинное направление реакции противоположно выбранному:

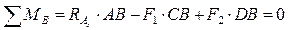
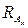, следовательно, и 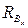найдены верно.

5. Строим эпюру крутящих моментов 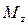(рис. 5.1,в).

6. Определяем в характерных сечениях значения изгибающих моментов в вертикальной плоскости и 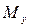в горизонтальной плоскости и строим эпюры (рис. 5.1, г, д):

;

;

;

.

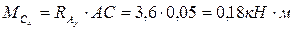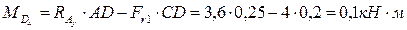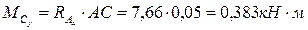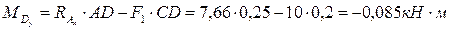7. Вычисляем наибольшее значение эквивалентного момента по заданным гипотезам прочности. Так как в данном примере значение суммарного изгибающего момента в сечении С больше, чем в сечении D,

;

,

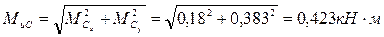то сечение С и является опасным. Определяем эквивалентный момент в сечении С.

Вариант а:

.

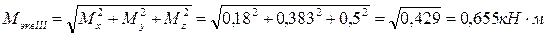Вариант б:

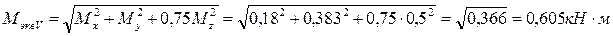
8. Определяем требуемые размеры вала по вариантам а и б.

По варианту а

.

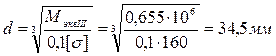По варианту б

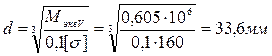
Принимаем .

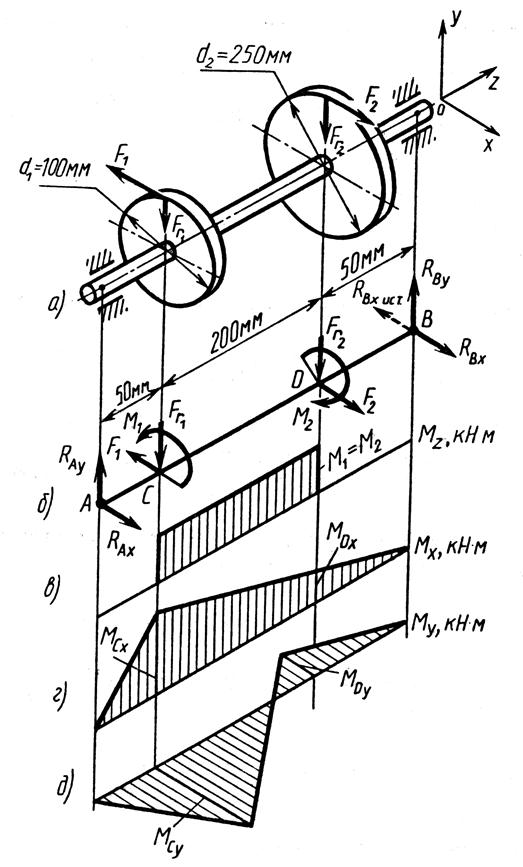
Рисунок 5.1

ВАРИАНТЫ ЗАДАНИЙ