Постановка задачи. Найти неопределенный интеграл
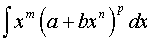 ,
,
где 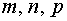 – рациональные числа.
– рациональные числа.
План решения. Выражение называется дифференциальным биномом. Условия его интегрируемости в элементарных функциях получены П.Л. Чебышевым. Интеграл
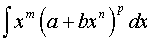
выражается через конечную комбинацию элементарных функций в следующих трех случаях:
1) 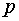 – целое число; в этом случае данный интеграл вычисляется простым разложением;
– целое число; в этом случае данный интеграл вычисляется простым разложением;
2) 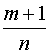 – целое число; в этом случае подстановка
– целое число; в этом случае подстановка 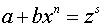 , где
, где 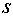 – знаменатель дроби
– знаменатель дроби 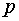 , приводит к интегралу от рациональной функции.
, приводит к интегралу от рациональной функции.
3) 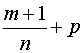 – целое число; в этом случае подстановка
– целое число; в этом случае подстановка 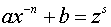 , где
, где 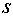 – знаменатель дроби
– знаменатель дроби 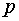 , приводит к интегралу от рациональной функции.
, приводит к интегралу от рациональной функции.
Задача 13. Найти неопределенные интегралы.
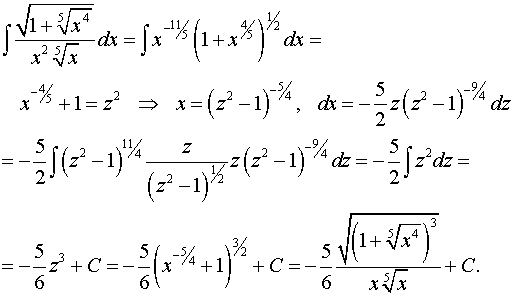
 2015-01-21
2015-01-21 419
419








