Постановка задачи. Вычислить площадь области, ограниченной графиками функций 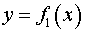 и
и 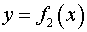 (
(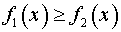 или
или 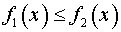 для всех точек области) и, возможно, прямыми
для всех точек области) и, возможно, прямыми 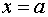 и
и 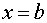 .
.
План решения. Если область 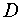 задана системой неравенств
задана системой неравенств
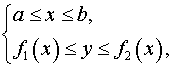
то площадь области находится по формуле 
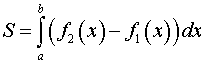 .
.
Если неравенства, определяющие область  , неизвестны, т.е. неизвестны
, неизвестны, т.е. неизвестны 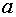 и
и 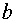 и неизвестно, какая из функций
и неизвестно, какая из функций 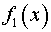 и
и 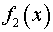 больше на
больше на 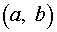 , то выполняем следующие операции.
, то выполняем следующие операции.
1. Находим 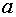 и
и 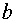 как абсциссы точек пересечения графиков функций
как абсциссы точек пересечения графиков функций 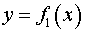 и
и 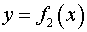 , т.е. решаем уравнение
, т.е. решаем уравнение
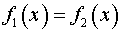 .
.
2. Исследуем знак разности 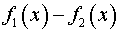 на
на 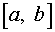 . Для этого достаточно вычислить значение
. Для этого достаточно вычислить значение 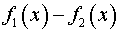 в какой-нибудь точке из
в какой-нибудь точке из 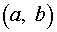 . Если оно положительно, то
. Если оно положительно, то 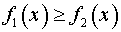 и
и
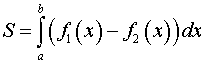 ;
;
если оно отрицательно, то 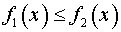 и
и
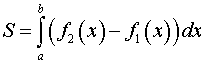 .
.
Замечание. Иногда бывает полезным построить график области 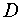 , ограниченной функциями
, ограниченной функциями 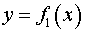 и
и 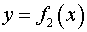 .
.
Задача 14. Вычислить площади фигур, ограниченных графиками функций.
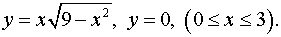
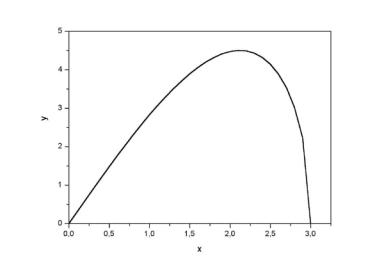
Строим график функции.
Вычисляем площадь.
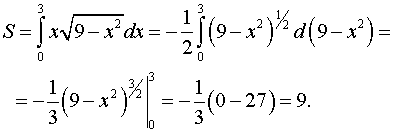
 2015-01-21
2015-01-21 1028
1028








