Интегрирование выражений и
и 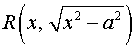 .
.
Постановка задачи. Найти неопределенные интегралы вида:
а) 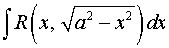 ;
;
б) 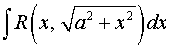 ;
;
в) 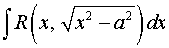 ;
;
где 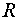 – рациональная функция.
– рациональная функция.
План решения.
1. Чтобы избавиться от радикала, используем тригонометрические или гиперболические подстановки:
а) 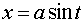 или
или 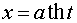 ;
;
б) 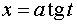 или
или 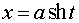 ;
;
в) 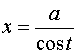 или
или 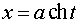 .
.
2. Применив формулу замены переменной, получим интегралы вида
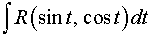 .
.
3. Вычисляем последний интеграл с помощью известных подстановок или методом понижения степени.
4. Возвращаемся к переменной 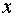 и записываем ответ.
и записываем ответ.
Замечание. В случае определенного интеграла все аналогично, только необходимо изменить пределы интегрирования соответствующим образом.
Задача 12. Вычислить определенные интегралы.
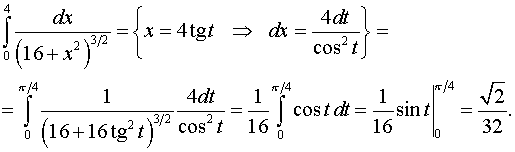
 2015-01-21
2015-01-21 418
418








