Основные свойства непрерывных функций

1. Если 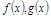непр. в т. 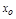, , 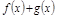, 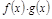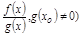непрерывны в т. .

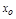Д-во: следует из теорем о пределах.

2. Пусть 1) 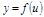непр-а. в т 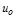; 2) 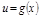непр. в т. ;

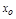3) 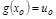, тогда ф-я 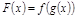непр. в т. .

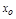Д-во: .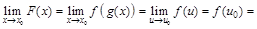

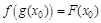3. Все элем-ные ф-и непрерывны в своей области опред-я.

4. Т. Больцано-Коши: Если 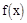непр. на 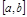и на концах отрезка принимает знач. разных знаков: 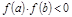, то найдется т.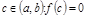

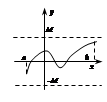ПР. Ур-е 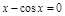имеет корень на 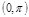, т.к. 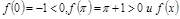– непр.

5. Если 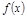непр. на 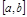, то она ограничена на 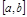, т.е. .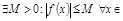

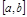6. Если 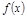непр. на 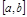и принимает на концах неравные зн-я 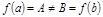, то она принимает все зн-я между A и B, т.е. пусть A<B, тогда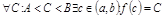

7. Т. Вейерштрасса: Если 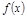непр. на 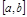, то существует ее наиб. и наим. значения на 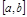, т.е. : .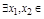

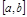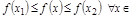
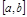Зам. в Т. Вей-са сущ-ны усл. непр. ф-и на .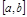

ПР. 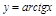. 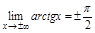, но наиб. и наим. значения ф-я не достигает из-за неогр. промежутка.

ПР. 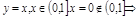ф-я не достигает наиб и наим. зн.

ПР. 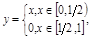– не достигает наиб. знач.

След. Непр. на 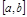ф-я принимает все промежуточные
зн-я между своими наиб. и наим. зн-ми на .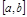

__________________________________________________

§ 12. Равномерная непрерывность функции. (сам-но)

Опр.1. Ф-я 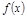, ограниченная на X, наз. равномерно непрерывной на X, если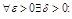

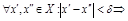
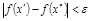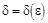. , но очевидно, что если 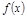опр. и непр. на 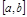, то она равн. непр. на нем.

ПР. 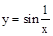– непр. на 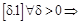и равн. непр. Но на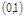 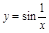не яв-ся равн. непр.