Пусть 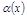 – б.м. при
– б.м. при 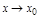 , тогда:
, тогда:
1.  , 2.
, 2. 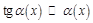 ,
,
3. 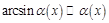 , 4.
, 4. 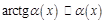
5.  , 6.
, 6. 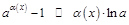
7. 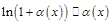 ,
,
8. 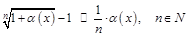 .
.
ПР. 1) 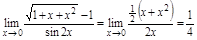 ;
;
2) 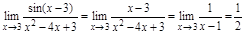 .
.
§10 Непрерывность функции.
Пусть ф-я 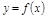 опр. в точке
опр. в точке 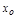 и в некоторой ее окрестности
и в некоторой ее окрестности 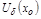 .
.
Изменим 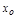 на
на 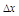 так, что
так, что 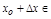
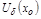 .
.
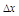 наз-ся приращением аргумента.
наз-ся приращением аргумента.
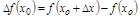 наз-ся приращением функции, соответствующим приращению аргумента
наз-ся приращением функции, соответствующим приращению аргумента 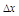 .
.
Опр.1. Ф-я 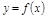 наз. непрерывной в т.
наз. непрерывной в т. 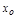 , если б.м.
, если б.м. 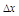 соответствует б.м.
соответствует б.м. 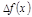 . т.е.
. т.е.  .
.
Расшифруем: 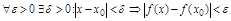 . Таким образом, получаем еще два эквивалентных определения:
. Таким образом, получаем еще два эквивалентных определения:
Опр.2. Ф-я 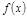 наз. непрерывной в т.
наз. непрерывной в т. 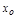 , если
, если 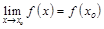 =
= 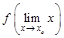 .
.
Т.о., получаем:
Опр.3. 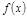 непр. в т.
непр. в т. 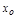
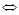 когда выполнено:
когда выполнено:
1) 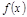 -опр. в точке
-опр. в точке 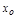 ;
;
2) 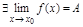 , т.е.
, т.е. 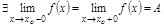 ;
;
3) 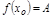 .
.
Опр.4. Если 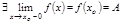

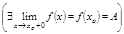 , то ф. наз. непр. слева (непр. справа) в т.
, то ф. наз. непр. слева (непр. справа) в т. 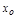 .
.
Опр.5. Ф-я 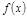 наз. непр. на отрезке
наз. непр. на отрезке 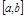 , если она непр. в каждой т.
, если она непр. в каждой т. 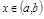 и непр. в т. a справа, в т. b – слева.
и непр. в т. a справа, в т. b – слева.
 2015-01-21
2015-01-21 289
289








