Глава 4. Введение в математический анализ
Опр.1. Пусть 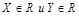 . Однозначное отображение
. Однозначное отображение 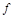 мн-ва
мн-ва 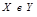 называется действительной функцией одного дейст. переменного. Обозначается:
называется действительной функцией одного дейст. переменного. Обозначается: 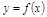 или
или 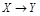 . Мн-во
. Мн-во 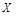 наз. областью опр-ния
наз. областью опр-ния
ф-и 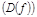 ; мн-во
; мн-во 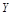 наз. областью значений ф-и.
наз. областью значений ф-и.  .
.
Способы задания функции:
1. Табличный
2. Графический
3. Аналитический:  ;
;
Опр.2. Основными элементарными ф-ми наз-ся следующие ф-ии: степенная, показательная, логарифмическая, тригоном-кие, обратные тригоном-кие.
Опр-я, св-ва и графики основных элем. ф-й – выучить !!!
Опр.3. Пусть 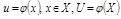 ,
, 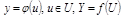 .
.
Тогда ф-ия 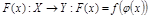 наз-ся сложной
наз-ся сложной
ф-ей или суперпозицией ф-ций 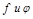 .
.
ПР. 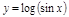 .
.
ПР. 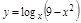 .
. 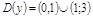 ,
, 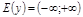 .
.
Опр.4. Элементарными ф-ми наз-ся ф-ции, которые получаются из основных элем-х ф-й с помощью четырех. ариф-х действий (сложения, вычитания, умножения, деления) и суперпозиций, применяемых конечное число раз.
Опр.5. Пусть имеется ф-я 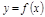 или f:
или f: 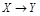 . Обратной по отношению к f наз. такая ф-я
. Обратной по отношению к f наз. такая ф-я 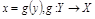 , что
, что 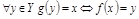 .Обоз.:
.Обоз.: 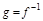 – обратная для
– обратная для 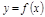 .
.
__________________________________________________
Т.о. для того, чтобы сущ-ла обратная ф-я, отображение д.б. взаимно однозначным. Графики взаимно обратных
ф-й симметричны от-но прямой y=x.
ПР. 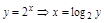 ;
; 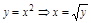 .
.
Опр.6. Задание функции в виде 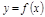 называется явным, а в виде
называется явным, а в виде 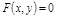 – неявным.
– неявным.
ПР. 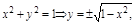
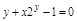 , y не выр-ся явно.
, y не выр-ся явно.
§ 2. Предел функции.
Опр.1. 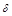 -окрестностью т.
-окрестностью т. 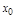 наз. интервал
наз. интервал 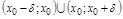
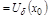 .
.
Опр.2. Последовательностью наз. ф-я, определенная на мн-ве N, т.е. посл-ть – ф-я натур. аргумента: 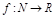 . Обозн.:
. Обозн.: 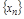 . Пр.
. Пр. 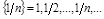
Опр.3. Число a наз. пределом послед. 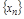 :
: 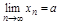
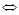
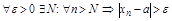 .
.
Геом. смысл предела послед.: 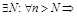
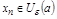 , т.е. вне
, т.е. вне 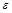 -окре-ти т. a окажется конечное число членов послед.
-окре-ти т. a окажется конечное число членов послед.
ПР. Док-ть, что 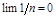 ;
; 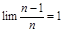 ;
; 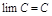 .
.
Опр.4. Послед., имеющая конечный предел, наз. сходящейся.
Пусть дана ф-ция 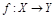 ,
, 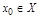 вместе с некоторой своей окрестностью, т.е.
вместе с некоторой своей окрестностью, т.е. 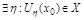 .
.
Опр. 5. Число 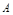 наз-ся пределом
наз-ся пределом  при
при 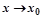 ,
, 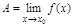 , если
, если 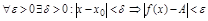 .
.
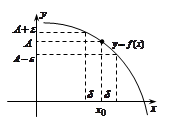 Пр. Д-ть, что
Пр. Д-ть, что  .
.
Д-во: нужно д-ть, что 
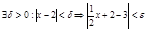 . Пусть
. Пусть 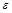 фиксировано. Тогда:
фиксировано. Тогда: 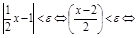
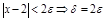 .
. 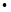
Зам. В опр. предела не требуется чтобы ф. была опр-на в т. 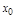 , достаточно, чтобы ф. была определена в окрест этой точки, т.е. ф. в точке не определена, а предел в этой т. может сущ-ть.
, достаточно, чтобы ф. была определена в окрест этой точки, т.е. ф. в точке не определена, а предел в этой т. может сущ-ть.
Опр. 6. Если ф-ция 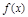 имеет пределом число
имеет пределом число 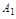 (
(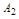 ) при доп. условии, что
) при доп. условии, что 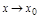 , оставаясь < (>)
, оставаясь < (>) 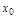 , то
, то 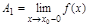 называется левым пределом (
называется левым пределом (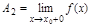 называется правым пределом). Правый и левый пределы наз-ся односторонними.
называется правым пределом). Правый и левый пределы наз-ся односторонними.
Пр. 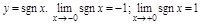 .
.
Т.1. (необх. и дост. условие сущ. предела ). Ф-я 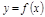 имеет предел при
имеет предел при 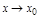 тогда и только тогда, когда сущ. лев. и пр. пределы при
тогда и только тогда, когда сущ. лев. и пр. пределы при 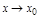 и они равны:
и они равны:
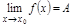
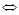
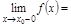
 .
.
Д-во: 
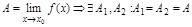 – очевидно
– очевидно
__________________________________________________

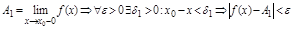 ;
;
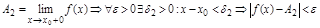 .
.
Возьмем 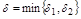 . Т.к.
. Т.к. 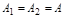 , то получим следующее:
, то получим следующее: 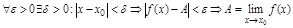 .
. 
ПР. 
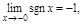
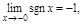

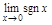 не сущ.
не сущ.
Опр.7. Если 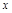 принимает любые значения, большие любого наперед заданного положительного числа, то говорят, что
принимает любые значения, большие любого наперед заданного положительного числа, то говорят, что  . Если
. Если 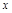 принимает любые значения, меньшие любого наперед заданного отрицательного числа, то говорят, что
принимает любые значения, меньшие любого наперед заданного отрицательного числа, то говорят, что 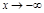 .
.
Опр.8.  .
.
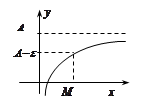
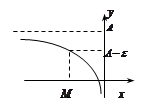 Опр.9.
Опр.9. 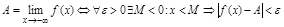 .
.
Опр.10. 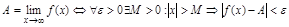
Пр. 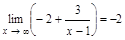 .
.
Опр. 11. 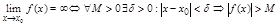 .
.
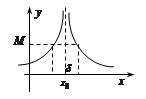 |
§3. Бесконечно малые и бесконечно большие величины.
Опр.1. Ф-я. 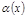 наз. б.м.в. при
наз. б.м.в. при 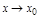 (
( ), если
), если 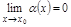
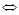
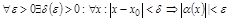
ПР. 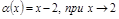 ;
; 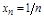 , есть б.м.в. при
, есть б.м.в. при  .
.
Опр.2. Ф-я. 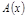 наз. б.б.в. при
наз. б.б.в. при 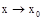 (
(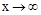 ), если
), если 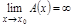
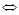
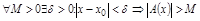 .
.
ПР. 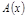
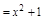 , при
, при  – есть б.б.в.
– есть б.б.в.
Т.2. (о связи б.м. и б.б.) Если 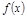 – б.б. при
– б.б. при 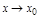 , то
, то 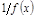 – б.м. при
– б.м. при 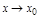 и наоборот.
и наоборот.
Д-во 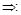 Дано
Дано 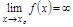
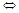
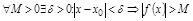
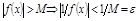

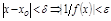
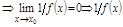 – б.м.,
– б.м., 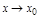 .
.
 сам-но!
сам-но! 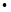
ПР
__________________________________________________
§4 Основные свойства бесконечно малых.
1. Сумма конечного числа б.м. есть б.м.
Док-во. Дано: 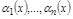 – б.м. Пусть n =2.
– б.м. Пусть n =2.
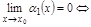
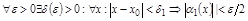
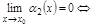
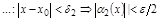 .
.
Выберем 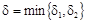

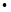
Опр.3. Ф-я 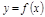 наз. ограниченной на нек-м мн-ве X, если
наз. ограниченной на нек-м мн-ве X, если 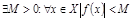 .
.
ПР. 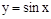 огр. на R.
огр. на R.
Опр.4. Ф-я 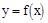 наз. ограниченнойпри
наз. ограниченнойпри 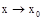 , если
, если 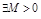
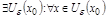
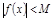 .
.
ПР.  огр. при
огр. при 
2. Произведение огр. при 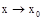 ф-и
ф-и 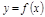 на б.м. при
на б.м. при 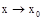 есть б.м. при
есть б.м. при 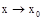 .
.
Д-во. Дано: 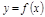 при
при 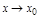 –огр.:
–огр.: 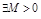 ,
, 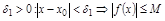
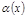 – б.м. при
– б.м. при 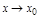 :
:
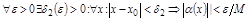 .
.
Зададим 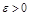 , обозначим
, обозначим 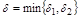

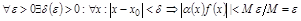
3. Произведение конечного числа б.м. при 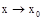 есть б.м. при
есть б.м. при 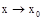 .
.
Д-во. Сам-но!
Т.3. (критерий существования предела ) 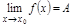
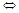
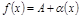 , где
, где 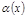
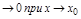 .
.
Док-во. «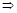 » Дано:
» Дано: 
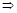
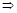
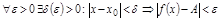 .
.
Пусть 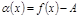 , тогда
, тогда 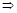
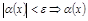 – б.м.в. и
– б.м.в. и 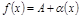
«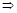 » Дано
» Дано 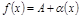 и
и 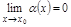
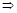
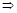
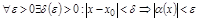 , но
, но 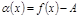
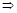
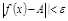
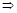
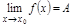 .
. 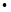
 2015-01-21
2015-01-21 327
327







