1. Пусть переменная величина x последовательно принимает значения
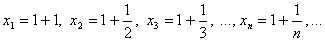
Докажем, что предел этой числовой последовательности равен 1. Возьмем произвольное положительное число ε. Нам нужно найти такое натуральное число N, что при всех n>N выполняется неравенство | xn - 1| < ε. Действительно, т.к.
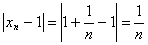 ,
,
то для выполнения соотношения |xn - a| < ε достаточно, чтобы 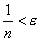 или
или 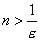 . Поэтому, взяв в качестве N любое натуральное число, удовлетворяющее неравенству
. Поэтому, взяв в качестве N любое натуральное число, удовлетворяющее неравенству 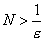 , получим что нужно. Так если взять, например,
, получим что нужно. Так если взять, например, 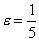 , то, положив N= 6, для всех n >6 будем иметь
, то, положив N= 6, для всех n >6 будем иметь 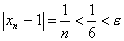 .
.
2. Используя определение предела числовой последовательности, доказать что 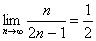 .
.
Возьмем произвольное ε > 0. Рассмотрим
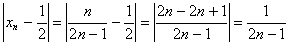 .
.
Тогда 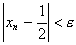 , если
, если 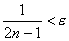 или
или 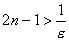 , т.е.
, т.е. 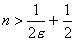 . Поэтому выберем любое натуральное число, удовлетворяющее неравенству
. Поэтому выберем любое натуральное число, удовлетворяющее неравенству 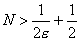 .
.
Сделаем несколько замечаний.
Замечание 1. Очевидно, что если все элементы числовой последовательности принимают одно и то же постоянное значение xn = c, то предел этой последовательности будет равен самой постоянной. Действительно, при любом ε всегда выполняется неравенство | xn - c | = | c - c | = 0 < ε.
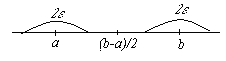 Замечание 2. Из определения предела следует, что последовательность не может иметь двух пределов. Действительно, предположим, что xn → a и одновременно xn → b. Возьмем любое
Замечание 2. Из определения предела следует, что последовательность не может иметь двух пределов. Действительно, предположим, что xn → a и одновременно xn → b. Возьмем любое 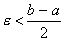 и отметим окрестности точек a и b радиуса ε (см. рис.). Тогда по определению предела, все элементы последовательности, начиная с некоторого, должны находиться как в окрестности точки а, так и в окрестности точки b, что невозможно.
и отметим окрестности точек a и b радиуса ε (см. рис.). Тогда по определению предела, все элементы последовательности, начиная с некоторого, должны находиться как в окрестности точки а, так и в окрестности точки b, что невозможно.
Замечание 3. Не следует думать, что каждая числовая последовательность имеет предел. Пусть, например, переменная величина принимает значения 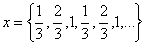 . Несложно заметить, что эта последовательность не стремится ни к какому пределу.
. Несложно заметить, что эта последовательность не стремится ни к какому пределу.
ПРЕДЕЛ ФУНКЦИИ Пусть функция y=f(x) определена в некоторой окрестности точки a. Предположим, что независимая переменная x неограниченно приближается к числу a. Это означает, что мы можем придавать х значения сколь угодно близкие к a, но не равные a. Будем обозначать это так x → a. Для таких x найдем соответствующие значения функции. Может случиться, что значения f(x) также неограниченно приближаются к некоторому числу b. Тогда говорят, что число b есть предел функции f(x) при x → a. Введем строгое определение предела функции. Функция y=f(x) стремится к пределу b при x → a, если для каждого положительного числа ε, как бы мало оно не было, можно указать такое положительное число δ, что при всех x ≠ a из области определения функции, удовлетворяющих неравенству | x - a | < δ, имеет место неравенство | f(x) - b | < ε. Если b есть предел функции f(x) при x → a, то пишут 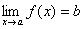 или f(x) → b при x → a. Проиллюстрируем это определение на графике функции. Т.к. из неравенства | x - a | < δ должно следовать неравенство | f(x) - b | < ε, т.е. при x Î (a - δ, a + δ) соответствующие значения функции f(x) Î (b - ε, b + ε), то, взяв произвольное ε > 0, мы можем подобрать такое число δ, что для всех точек x, лежащих в δ – окрестности точки a, соответствующие точки графика функции должны лежать внутри полосы шириной 2ε, ограниченной прямыми y = b – ε и y = b + ε. Несложно заметить, что предел функции должен обладать теми же свойствами, что и предел числовой последовательности, а именно или f(x) → b при x → a. Проиллюстрируем это определение на графике функции. Т.к. из неравенства | x - a | < δ должно следовать неравенство | f(x) - b | < ε, т.е. при x Î (a - δ, a + δ) соответствующие значения функции f(x) Î (b - ε, b + ε), то, взяв произвольное ε > 0, мы можем подобрать такое число δ, что для всех точек x, лежащих в δ – окрестности точки a, соответствующие точки графика функции должны лежать внутри полосы шириной 2ε, ограниченной прямыми y = b – ε и y = b + ε. Несложно заметить, что предел функции должен обладать теми же свойствами, что и предел числовой последовательности, а именно 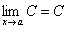 и если при x → a функция имеет предел, то он единственный. Примеры. 1. Найти предел функции y =2 x +1 при x → 1. Используя график функции, можно увидеть, что если x → 1 с любой стороны, то соответствующие точки M (x, y) графика стремятся к точке M (1, 3), т.е. можно предположить, что и если при x → a функция имеет предел, то он единственный. Примеры. 1. Найти предел функции y =2 x +1 при x → 1. Используя график функции, можно увидеть, что если x → 1 с любой стороны, то соответствующие точки M (x, y) графика стремятся к точке M (1, 3), т.е. можно предположить, что 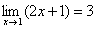 . Докажем это. Зададим произвольное число ε > 0. Нам нужно, чтобы выполнялось неравенство |(2 x+ 1) – 3 |< ε или |2 x –2| < ε, откуда | x – 1| < ε. Таким образом, если положить δ = ε/2, то при всех x, удовлетворяющих неравенству |x – 1 |< δ, будет выполняться неравенство | y – 3| < ε. По определению предела это и означает, что 3 есть предел функции y =2 x +1 при x → 1. 2. Найти предел функции y =ex+1 при x → 0. Используя график заданной функции, несложно заметить, . Докажем это. Зададим произвольное число ε > 0. Нам нужно, чтобы выполнялось неравенство |(2 x+ 1) – 3 |< ε или |2 x –2| < ε, откуда | x – 1| < ε. Таким образом, если положить δ = ε/2, то при всех x, удовлетворяющих неравенству |x – 1 |< δ, будет выполняться неравенство | y – 3| < ε. По определению предела это и означает, что 3 есть предел функции y =2 x +1 при x → 1. 2. Найти предел функции y =ex+1 при x → 0. Используя график заданной функции, несложно заметить, 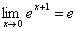 . . |  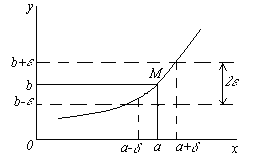 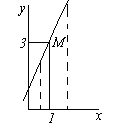 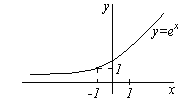 |
 2015-01-21
2015-01-21 884
884








