Для конечного участка потока 1-2 уравнение энергии имеет вид:
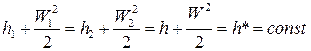 , (1)
, (1)
где h* - полная энтальпия, или энтальпия адиабатного торможения при скорости потока W =0. Таким образом, при движении газа его полная энергия, состоящая из кинетической энергии видимого движения и энергии, выражаемой энтальпией h=u+pv, остается постоянной. Всякое изменение кинетической энергии вызывает соответствующее изменение его энтальпии, а, следовательно, и температуры. В соплах скорость увеличивается, а температура уменьшается. В диффузорах скорость уменьшается, а температура увеличивается.
При полном торможении потока (w =0) температура принимает наибольшее значение и называется температурой полного торможения Т *. Для идеального газа ср =const, h=cpT и h*=cpT*. Тогда из уравнения (1) следует, что:
cpT*=cpT+ 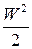 , или
, или 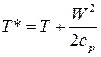 , (2)
, (2)
где Т – статическая температура (температура движущейся среды). В уравнении (2) второй член правой части преобразуем к следующему виду:
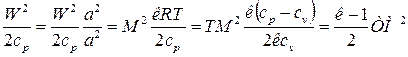 ,
,
где R=cp-cv по уравнению Майера; cp=кcv, M =W/a – число Маха; a 2 =кRT;
а – скорость звука. Тогда окончательно получим выражение для расчета скорости торможения:
Т*=Т 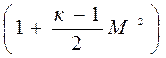 . (3)
. (3)
Расчет давления торможения проводится по формуле:
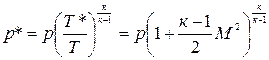 . (4)
. (4)
Плотность заторможенного потока будет равна:
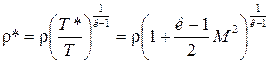 . (5)
. (5)
Для расчета параметров можно использовать таблицы газодинамических функций, которые облегчают решение задач. При этом вводится приведенная скорость 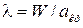 , где критическая скорость
, где критическая скорость 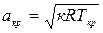 , а
, а 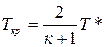 . Тогда получим:
. Тогда получим:
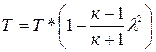 и газодинамическая функция
и газодинамическая функция 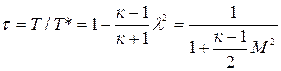 .
.
Функция 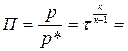
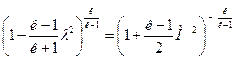 .
.
Функция 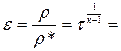
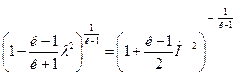 .
.
Располагая таблицами, в которых для каждого значения 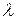 или М указаны значения функций
или М указаны значения функций 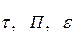 , можно быстро переходить от действительных (термодинамических) параметров потока к параметрам торможения и обратно. Выбор для расчета чисел М или
, можно быстро переходить от действительных (термодинамических) параметров потока к параметрам торможения и обратно. Выбор для расчета чисел М или 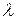 определяется удобствами применения в каждом конкретном случае. Для определения расхода газа через произвольный канал по известной площади проходного сечения f, числу М или
определяется удобствами применения в каждом конкретном случае. Для определения расхода газа через произвольный канал по известной площади проходного сечения f, числу М или 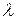 и по параметрам заторможенного потока можно воспользоваться газодинамической функцией
и по параметрам заторможенного потока можно воспользоваться газодинамической функцией 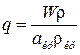 , которая возрастает с ростом числа М при М <1, достигает максимума q max=1 при М =
, которая возрастает с ростом числа М при М <1, достигает максимума q max=1 при М = 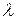 =1 и снова убывает при M >1.
=1 и снова убывает при M >1.
Тогда уравнение расхода 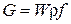 можно записать в виде
можно записать в виде 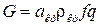 , где
, где 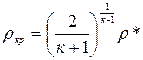 и
и 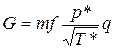 , где
, где 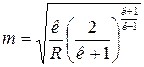 , т.е.
, т.е. 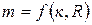 . Для воздуха к =1,4, R =297 Дж/кгК, m =0.3965.
. Для воздуха к =1,4, R =297 Дж/кгК, m =0.3965.
Например, при определении изменения параметров потока газа по длине сопла, принимая р 1= р* и Т 1= Т* при заданном значении показателя адиабаты к и известных геометрических размерах сопла и расхода G можно определить изменение массовой скорости 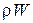 по длине сопла, величину акр
по длине сопла, величину акр 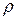 кр и функцию q. Далее по таблицам при заданном к можно определить функции
кр и функцию q. Далее по таблицам при заданном к можно определить функции 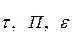 и величины
и величины 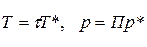 и
и 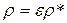 .
.
 2015-01-21
2015-01-21 7193
7193
