Найдите 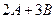 , где
, где 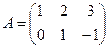 ,
, 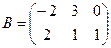 .
.

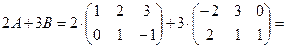
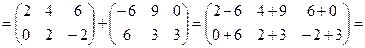

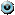
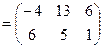 .
.
Умножение матриц. Произведением матрицы 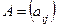 размерности
размерности 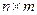 на матрицу
на матрицу 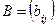 размерности
размерности 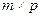 называется матрица
называется матрица 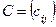 размерности
размерности 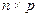 такая, что
такая, что 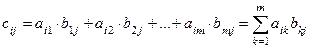 ,
, 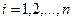 ,
, 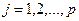 .
.
 Умножать матрицы
Умножать матрицы 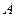 и
и 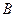 можно лишь в том случае, когда число столбцов первого сомножителя
можно лишь в том случае, когда число столбцов первого сомножителя 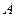 (число элементов в каждой строке матрицы
(число элементов в каждой строке матрицы 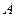 ) совпадает с числом строк второго сомножителя
) совпадает с числом строк второго сомножителя 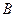 (число элементов в каждом столбце
(число элементов в каждом столбце 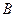 ). В частности для квадратных матриц одинакового порядка определены оба произведения
). В частности для квадратных матриц одинакового порядка определены оба произведения 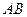 и
и 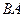 , и матрицы произведения являются матрицами того же порядка
, и матрицы произведения являются матрицами того же порядка
Пример 1.9. Пусть 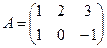 ,
, 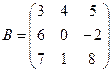 . Найдите произведения
. Найдите произведения 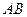 и
и 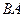 (если это возможно).
(если это возможно).



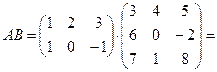


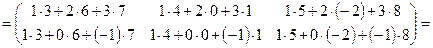
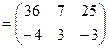 .
.
 Произведение
Произведение 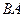 не существует, так как число столбцов матрицы
не существует, так как число столбцов матрицы 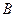 не совпадает с числом строк матрицы
не совпадает с числом строк матрицы 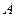
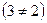 .
.
Пример 1.10. Пусть 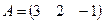 ,
, 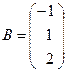 . Найдите произведения
. Найдите произведения 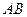 и
и 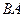 (если это возможно).
(если это возможно).

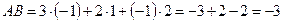 .
.

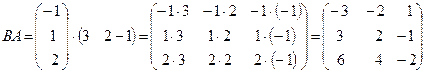 .
.

 Из приведенных выше примеров ясно, что в общем случае
Из приведенных выше примеров ясно, что в общем случае 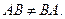 .
.
Коммутирующими называют матрицы 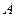 и
и 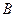 , если для них выполнено условие
, если для них выполнено условие 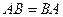 .
.
 Свойства операции умножения матриц:
Свойства операции умножения матриц:
а) ассоциативность: если определено одно из произведений 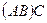 или
или 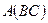 , то определено также и второе произведение, и имеет место выше приведённое равенство
, то определено также и второе произведение, и имеет место выше приведённое равенство 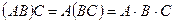 ;
;
б) дистрибутивность: если 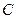 — такая матрица, что определено произведение
— такая матрица, что определено произведение 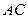 , то определены произведения
, то определены произведения 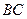 и
и 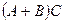 и верно равенство
и верно равенство 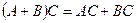 (
(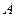 и
и 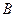 — матрицы одинаковых размеров);
— матрицы одинаковых размеров);
в) дистрибутивность: если 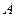 — такая матрица, что определено произведение
— такая матрица, что определено произведение 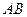 , то определены произведения
, то определены произведения 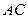 и
и 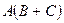 и верно равенство
и верно равенство 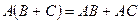 (
(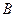 и
и 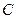 — матрицы одинаковых размеров);
— матрицы одинаковых размеров);
г) 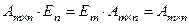 .
.

 2015-01-21
2015-01-21 476
476








