Механика — часть физики, которая изучает закономерности механического движения и причины, вызывающие или изменяющие это движение. Механическое движение — это изменение с течением времени взаимного расположения тел или их частей.
Развитие механики как науки начинается с III в. до н. э., когда древнегреческий ученый Архимед (287—212 до н. э.) сформулировал закон равновесия рычага и законы равновесия плавающих тел. Основные законы механики установлены итальянским физиком и астрономом Г. Галилеем (1564—1642) и окончательно сформулированы английским ученым И. Ньютоном (1643—1727).
Механика Галилея—Ньютона называется классической механикой. В ней изучаются законы движения макроскопических тел, скорости которых малы по сравнению со скоростью света в вакууме. Законы движения макроскопических тел со скоростями, сравнимыми со скоростью с, изучаются релятивистской механикой, основанной на специальной теории относительности, сформулированной А. Эйнштейном (1879—1955). Для описания движения микроскопических тел (отдельные атомы и элементарные частицы) законы классической механики неприменимы — они заменяются законами квантовой механики.
В первой части нашего курса мы будем изучать механику Галилея—Ньютона, т. е. рассматривать движение макроскопических тел со скоростями, значительно меньшими скорости с. В классической механике общепринята концепция пространства и времени, разработанная И. Ньютоном и господствовавшая в естествознании на протяжении XVII—XIX вв. Механика Галилея—Ньютона рассматривает пространство и время как объективные формы существования материи, но в отрыве друг от друга и от движения материальных тел, что соответствовало уровню знаний того времени.
Механика делится на три раздела: 1) кинематику; 2) динамику; 3) статику.
Кинематика изучает движение тел, не рассматривая причины, которые это движение обусловливают.
Динамика изучает законы движения тел и причины, которые вызывают или изменяют это движение.
Статика изучает законы равновесия системы тел. Если известны законы движения тел, то из них можно установить и законы равновесия. Поэтому законы статики отдельно от законов динамики физика не рассматривает.
Механика для описания движения тел в зависимости от условий конкретных задач использует разные физические модели. Простейшей моделью является материальная точка — тело, обладающее массой, размерами которого в данной задаче можно пренебречь. Понятие материальной точки — абстрактное, но его введение облегчает решение практических задач. Например, изучая движение планет по орбитам вокруг Солнца, можно принять их за материальные точки.
Произвольное макроскопическое тело или систему тел можно мысленно разбить на малые взаимодействующие между собой части, каждая из которых рассматривается как материальная точка. Тогда изучение движения произвольной системы тел сводится к изучению системы материальных точек. В механике сначала изучают движение одной материальной точки, а затем переходят к изучению движения системы материальных точек.
Под воздействием тел друг на друга тела могут деформироваться, т. е. изменять свою форму и размеры. Поэтому в механике вводится еще одна модель — абсолютно твердое тело. Абсолютно твердым телом называется тело, которое ни при каких условиях не может деформироваться и при всех условиях расстояние между двумя точками (или точнее между двумя частицами) этого тела остается постоянным.
Любое движение твердого тела можно представить как комбинацию поступательного и вращательного движений. Поступательное движение — это движение, при котором любая прямая, жестко связанная с движущимся телом, остается параллельной своему первоначальному положению. Вращательное движение — это движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения.
Движение тел происходит в пространстве и во времени. Поэтому для описания движения материальной точки надо знать, в каких местах пространства эта точка находилась и в какие моменты времени она проходила то или иное положение.
Положение материальной точки определяется по отношению к какому-либо другому, произвольно выбранному телу, называемому телом отсчета. С ним связывается система отсчета — совокупность системы координат и часов, связанных с телом от счета. В декартовой системе координат, используемой наиболее часто, положение точки А в данный момент времени по отношению к этой системе характеризуется тремя координатами x,yuz или радиусом-вектором г, проведенным из начала системы координат в данную точку (рис. 1).
При движении материальной точки ее координаты с течением времени изменяются.
В общем случае ее движение определяется скалярными уравнениями.
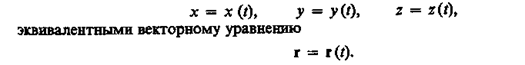
(1.1, 1.2)
Уравнения (1.1) и соответственно (1.2) называются кинематическими уравнениями движения материальной точки.
Число независимых координат, полностью определяющих положение точки в пространстве, называется числом степеней свободы. Если материальная точка свободно движется в пространстве, то, как уже было сказано, она обладает тремя степенями степенями свободы, если вдоль некоторой линии, то одной степенью свободы.

Рис. 1
Исключая t вуравнениях (1.1) и (1.2), получим уравнение траектории движения материальной точки. Траектория движения материальной точки — линия, описываемая этой точкой в пространстве. В зависимости от формы траектории движение может быть прямолинейным или криволинейным.
Рассмотрим движение материальной точки вдоль произвольной траектории (рис. 2). Отсчет времени начнем с момента, когда точка находилась в положении А. Длина участка траектории АВ, пройденного материальной точкой с момента начала отсчета времени, называется длиной пути aj и является скалярной функцией времени: Ds = Ds(t). Вектор Dr = r – r0, проведенный из начального положения движущейся точки в положение ее в данный момент времени (приращение радиуса-вектора точки за рассматриваемый промежуток времени), называется перемещением.
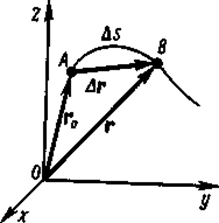
Рис. 2
При прямолинейном движении вектор перемещения совпадает с соответствующим участком траектории и модуль перемещения |Dr| равен пройденному пути Ds.
 2015-01-21
2015-01-21 1208
1208








