Обобщенной координатой механической системы (механизма) называется независимая координата, однозначно определяющая положение системы в пространстве.
Число обобщенных координат определяет число степеней свободы системы.
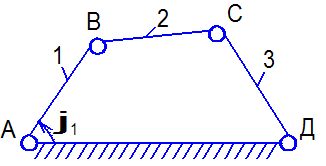
Рис. 1.6
Свободное твердое тело (звено) в пространстве обладает 6 степенями свободы, т.е. оно может совершать 3 независимых поступательных движения вдоль взаимно-перпендикулярных осей и 3 вращательных движения вокруг тех же осей.
Если же звено входит в кинематическую пару, то на относительное движение его, т.е. на движение по отношению ко второму звену, входящему в эту пару накладываются определенные ограничения. Эти ограничения называются условиями связи - S.
По числу условий связи, накладываемых на относительные движения звеньев, пары подразделяются на классы.
Класс кинематической пары соответствует числу условий связи, накладываемых на относительное движение звеньев, входящих в эту пару.
В зависимости от способа соединения звеньев в кинематическую пару число условий связи может меняться от 1 до 5.
Поэтому все кинематические пары можно разделить на 5 классов.
К I классу относятся пары, накладывающие на относительное движение звеньев одно условие (5-ти подвижные пары).
Ко II классу относятся пары, накладывающие два условия (4-х подвижные) и т.д.
Если на движение звена в пространстве, не наложено ни каких условий связи, то оно обладает 6 степенями свободы.
Тогда, если число звеньев кинетической цепи - К, то общее число степеней свободы, которым обладают К звеньев до их соединения в кинетическую цепь - 6 К
 (степень свободы) до соединения в кинематическую цепь.
(степень свободы) до соединения в кинематическую цепь.
Соединение звеньев в кинематическую цепь накладывает различное число связей на относительное движение звеньев, зависящее от класса пар. Если число пар I класса обозначить P1, II класса – P2, III класса – P3, IV класса – P4, V класса – P5,
то из 6к степеней свободы, которыми обладали звенья до их вхождения в кинематические пары, необходимо исключить те степени свободы, которые отнимаются вхождением звеньев в кинематические пары.
Тогда число степеней свободы Н, которым обладает кинематическая цепь будет равно:
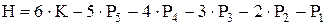 | (1.1) |
Если одно из звеньев кинематической цепи будет неподвижным, то общее число степеней свободы цепи уменьшится на 6 и число степеней свободы W относительно неподвижного звена будет равно:
 | (1.2) |
Число W степеней свободы кинематической цепи относительно стойки называется числом степеней неподвижности (степенью неподвижности) кинематической цепи.
Подставляя (1.1) во (1.2):
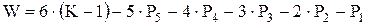
если обозначить ( ) через n то получим:
) через n то получим:
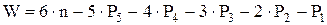
где n - число подвижных звеньев кинематической цепи.
Это равенство носит название формулы подвижности или формула Сомова-Малышева.
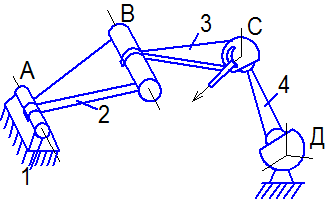 |
| а) кинематическая цепь |
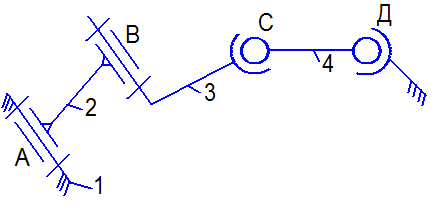 |
| б) схема кинематической цепи |
| Рис. 1. 7 |
| Звенья 1 и 2 - входят в к.пару A (V кл.) |  |
| 2 и 3 - в пару В (V кл.) | |
| 3 и 4 - в пару С (IV кл.) |  |
| 4 и 5 - в пару D (III кл.) |  |
 | |
 | |
 |
Подставим в формулу и получим
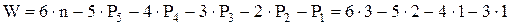
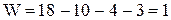
Степень свободы (подвижности) механизма показывает, сколько надо задать независимых координат, чтобы характеризовать положение любого звена механизма относительно стойки.
Если механизм обладает  , то при заданном движении одного из звеньев (ведущего) все остальные звенья будут иметь вполне определенные движения.
, то при заданном движении одного из звеньев (ведущего) все остальные звенья будут иметь вполне определенные движения.
Если  , то определенность движения звеньев может быть обеспечена или двумя ведущими звеньями имеющим по одному независимому движению, или одним ведущим звеном, имеющим 2 независимых движения (двухподвижных).
, то определенность движения звеньев может быть обеспечена или двумя ведущими звеньями имеющим по одному независимому движению, или одним ведущим звеном, имеющим 2 независимых движения (двухподвижных).
Выделим формулу для определения числа степеней свободы плоского механизма, звенья которого совершают движения параллельно одной какой-либо плоскости.
В этом случаи из 6 движений, которое каждое отдельное звено может совершать в пространстве, исключаются 3 движения - одно поступательное и два вращательных.
Следовательно, звено в плоскости может совершать только 3 движения.
При этом условии в состав плоских кинематических цепей могут входить лишь кинематические пары 4 и 5-го классов, т.е. кинематическая пара 5 кл. лишает 2-х из 3-х оставшихся движений, а кинематическая пара 4 кл. - 1 простейшего движения.
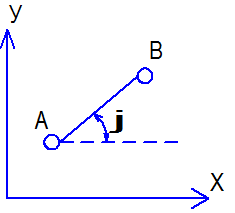
Рис. 1.8
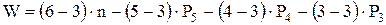
то степень подвижности плоского механизма:
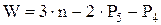 - структурная формула плоского механизма или формула Чебышева.
- структурная формула плоского механизма или формула Чебышева.
В состав плоских механизмов пары 1,2 и 3 кл. входить не могут. Кинематические пары 5 к. входящие в состав плоского механизма могут быть в 2-х видах:- либо в виде вращательной пары либо в виде поступательной пары. (т.е. низшие).
Кинематические пары 4 кл. - являются высшими кинематическими парами имеющими 2 степени свободы.
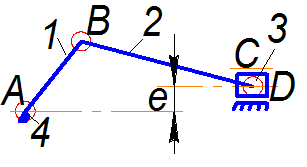
Рис. 1.9

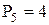
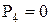
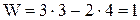
 2015-01-22
2015-01-22 1947
1947
