Пример 1 (кривошипно – ползунный механизм).
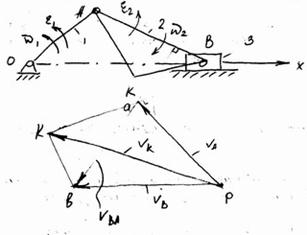 Известны размеры звеньев, положение
Известны размеры звеньев, положение
механизма, закон движения начального
звена (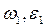 ).
).
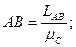
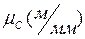 ;
; 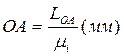
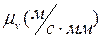 ;
; 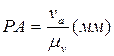
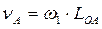
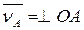 в сторону
в сторону 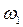
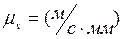 находим отрезок РА:
находим отрезок РА:
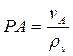
На основании теоремы о сложении скоростей в плоскопараллельном движении:
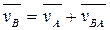 , где
, где 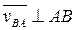 - относительная скорость точки В при вращении звена “2” вокруг точки “A”.
- относительная скорость точки В при вращении звена “2” вокруг точки “A”.
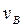 параллельна оси “X”. Это уравнение решаем графически путем построения плана скоростей.
параллельна оси “X”. Это уравнение решаем графически путем построения плана скоростей.
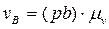 ;
; 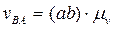
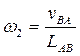 .
.
Направление 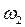 указывает вектор
указывает вектор 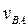
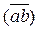 , если перенести его точку “B” и рассмотреть движение звена “2” вокруг точки “A”.
, если перенести его точку “B” и рассмотреть движение звена “2” вокруг точки “A”.

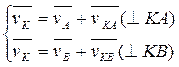
Решаем графически:
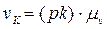
Свойства планов скоростей.
1) Отрезки, выходящие из полюса, выражают абсолютные скорости точки.
2) Отрезки, соединяющие концы векторов абсолютных скоростей, изображают относительные скорости 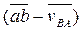 .
.
3) Теорема подобия: концы векторов абсолютных скоростей точек, принадлежащих одному звену, образуют фигуру, подобную соответствующей фигуре звена и сходственно с нею расположенную.
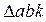 и
и 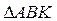 - подобны.
- подобны.
Сходственное расположение обозначает, что направление обхода одноименных контуров совпадают.
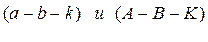 - по часовой стрелке.
- по часовой стрелке.
Ускорение 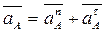
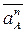 - от т.”A” к “O”
- от т.”A” к “O”
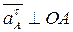 в сторону
в сторону 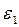
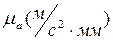 - масштабный коэффициент.
- масштабный коэффициент.
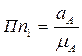 ;
; 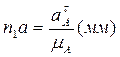
Построение:
Ускорение точки “B”:
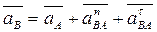
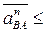 от “В” к “А”.
от “В” к “А”.
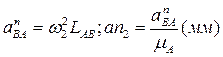
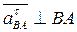 ;
; 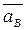 параллельно “Х”.
параллельно “Х”.
Решаем графически:
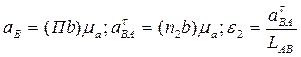
Направление 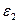 указывает вектор
указывает вектор 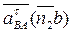 , если перенести его в точку “B” и рассмотреть движение точки “B” относительно “A”.
, если перенести его в точку “B” и рассмотреть движение точки “B” относительно “A”.
Точку “k” находим по свойству подобия, которое справедливо и для плана ускорений. Для этого методом засечек строим треугольник 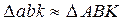 и сходственно с ним расположенный:
и сходственно с ним расположенный:
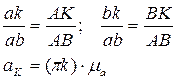
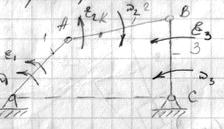
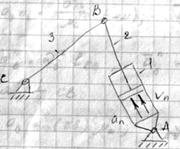
Пример 2 (четырехшарнирный механизм).
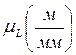 - масштабный коэффициент
- масштабный коэффициент
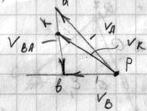
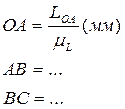
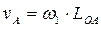
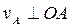 в сторону
в сторону 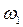
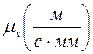 - коэффициент скоростей
- коэффициент скоростей
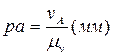 - отрезок в миллиметрах
- отрезок в миллиметрах
По теореме сложения скоростей: 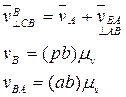
Угловые ускорения: 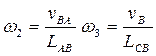
Точку “K” определяем по теореме подобия: 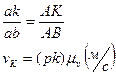
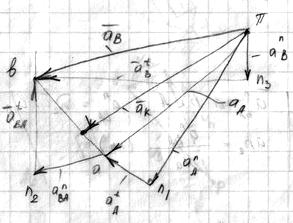
Определение ускорений: 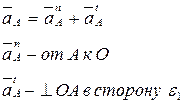
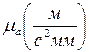 - масштабный коэффициент ускорений
- масштабный коэффициент ускорений
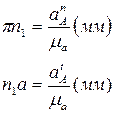
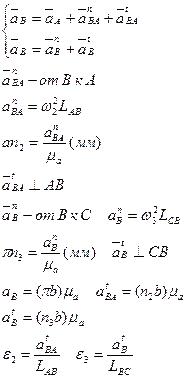
Точку “K” находим по теореме подобия:
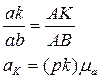
 Пример 3 (кулисный механизм).
Пример 3 (кулисный механизм).
Заданными являются относительное движение поршня “2” по
отношению к цилиндру “1” (скорость νn и ускорение поршня an).
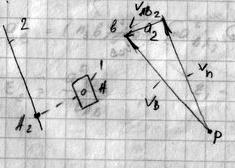
Далее будем рассматривать кинематически эквивалентную схему.
Различаем точки “A” и “A2”. А – неподвижная точка – центр
вращательной пары; А2 – точка, принадлежащая звену “2”
и в данный момент совпадающая с точкой “A”.
 Рассматриваем движение звена “2” как сложное, которое складывается из переносного (вращательного) движения вместе со звеном “1” и относительного (поступательного) по отношению к звену “1”:
Рассматриваем движение звена “2” как сложное, которое складывается из переносного (вращательного) движения вместе со звеном “1” и относительного (поступательного) по отношению к звену “1”:
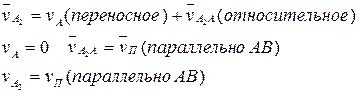

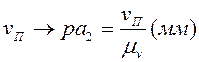
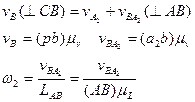
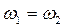 - общее переносное движение
- общее переносное движение
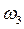 - вращение “B” вокруг “C”
- вращение “B” вокруг “C”
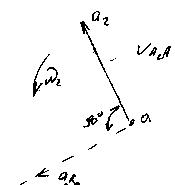
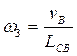
Находим ускорения:
Ускорение точки “A2”:
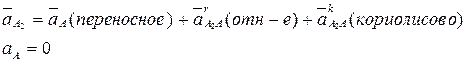
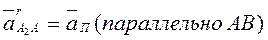 - заданное относительное ускорение
- заданное относительное ускорение
В общем случае:
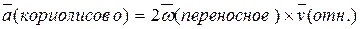
Для плоских механизмов угол между ωпер и νотн равен 900. Тогда:
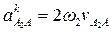
Направление 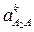 указывает вектор относительной скорости
указывает вектор относительной скорости 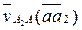 , повернутый на 900 в сторону ω2.
, повернутый на 900 в сторону ω2.
Отрезок, изображающий аП, равен:
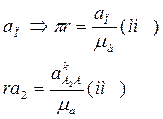
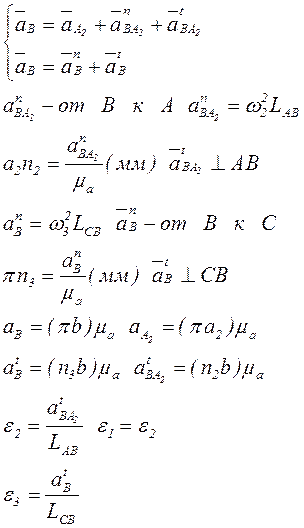
 2015-01-30
2015-01-30 1749
1749








