2015-01-30
1266
Пример 1 (кривошипно – ползунный механизм).
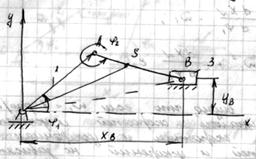Известно:
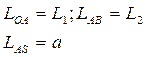
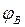- эксцентриситет
(смещение);
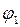- обобщенная координата.
Решение.
Используем метод замкнутых векторных контуров.
Контур ОА ВО:
Проецируем это уравнение на оси координат:
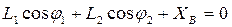(1)
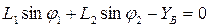(2)
Из (2) находим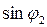 
:
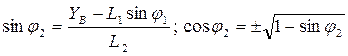
Знак “+”, если ползун “3” находится справа от центра “O”.
Знак “-”, если ползун “3” находится слева от центра “O”.
После нахождения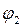 
определяем 
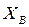из (1):
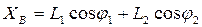
Дифференцируем уравнения (1) и (2) по обобщенной координате 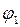. При этом:
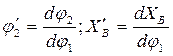
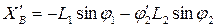(3)
Проекция на ось “Y”:
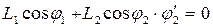(4)
Из (4) находим аналог угловой скорости звена “2”:
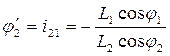
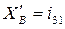
Дифференцируем (3) и (4) по :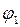
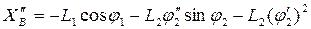(5)
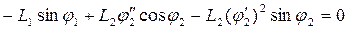(6)
Из (6) находим аналог углового ускорения звена “2”:
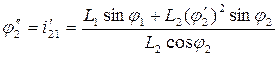
Из (5):
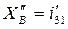
Для точки “3” можно записать:
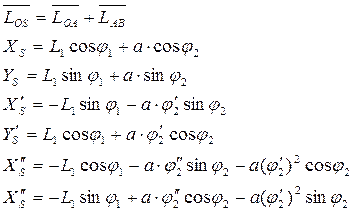
Зная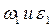 
, можно найти все скорости и ускорения:
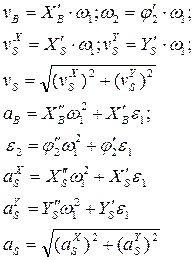
Получим приближенные формулы, когда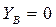 
:
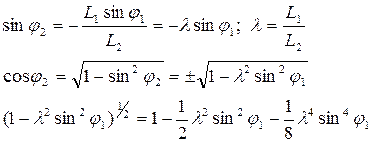
При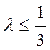 
можно ограничиться первыми двумя членами ряда:
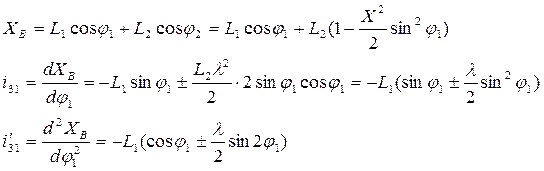
ОТВЕТ.
Пример 2.
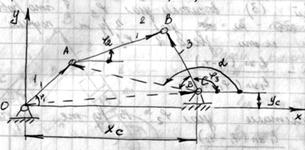
Имеем замкнутый контур OABC:
Составляем уравнение его контурности:
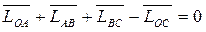
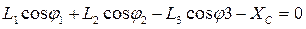(1)
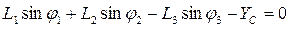(2)
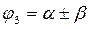, где “+” – если обход контура АВС будет против часовой стрелки,
где “-” – если обход контура АВС будет по часовой стрелке.
“β” находим из ∆ АВС по тереме косинусов:
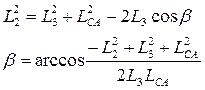
После определения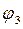 
определяются 
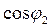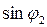, и угол 
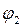из (1) и (2).
Дифференцируем (1) по :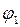
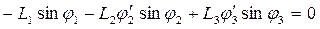(3)
Из всех углов в уравнении (3) вычитаем угол 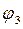, что равносильно повороту осей координат на этот угол. Получаем аналог угловой скорости звена “2”:
Далее вычитаем :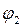
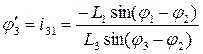
Дифференцируем (3) по :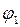
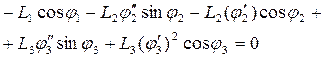(4)
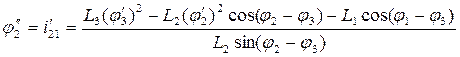
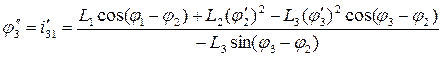
Пример 3 (кулисный механизм).
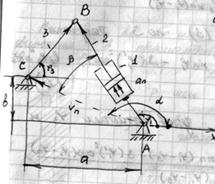
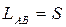- обобщенная
координата.
Используем метод замкнутых векторов.
Берем контур АВСА:
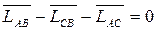
Проецируем это уравнение на оси координат:
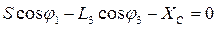(1)
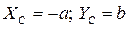
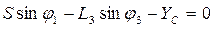(2)
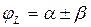, где “+” – если по часовой стрелке, а “-” – против часовой стрелки.
По теореме косинусов:
∆ АВС: 
Дифференцируем (1) по “S”:
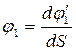- аналог угловой скорости звена “1”.
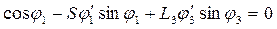(3)
Вычитаем угол :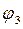
Вычитаем угол :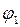
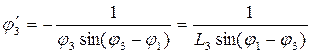
Дифференцируем (3) по “S”:
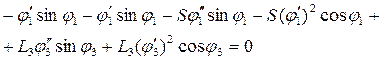(4)
Вычитаем из угла 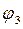. Тогда аналог:
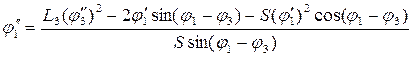
Вычитаем :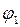
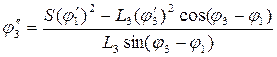
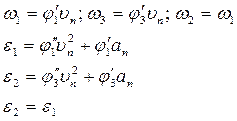
Кинематика винтового механизма.
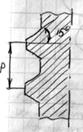“Р” – шаг резьбы.
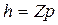- ход винта
“Z” – число заходов
Чаще всего используется трапецеидальная резьба.
При повороте винта на один оборот (2π радиан) он переместится вдоль оси на величину h относительно неподвижной гайки. При повороте на угол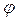 
переместится на расстояние S.
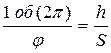
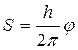
Скорость поступательного перемещения винта:
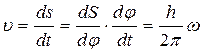
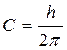- параметр винта (отношение линейной скорости к угловой).
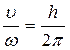
Различают винты с правой и левой винтовой линиями.
Во многих металлообрабатывающих применяется механизм, в котором ходовой винт “1” поступательно перемещает невращающуюся гайку “2”
1 – 0 – вращающаяся пара.
1 – 2 – винтовая пара.
2 – 0 – поступательная пара.
Для винтовой пары можем записать:
откуда передаточная функция:
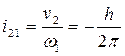
Вывод: в случае правого винта (h>0) ν1 и ω1 имеют противоположное направление.
