Силовой расчет манипулятора

Эта задача состоит в определении реактивных сил и моментов в кинематических парах, а также движущих сил и моментов приводных двигателей. Эта задача решается методом кинетостатики, основанном на принципе Даламбера.

Главный вектор сил инерции звена:

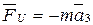
Главный момент сил инерции определяется в подвижной системе координат, связанной со звеном:

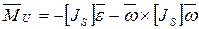
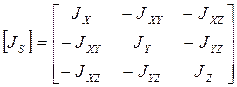- тензор инерции в центре масс.

Осевые моменты инерции:

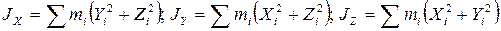
Центральные моменты инерции:

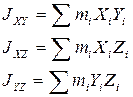
Если координатные оси совпадают с главными центральными осями инерции, то центробежные моменты инерции равны нулю. Такими осями являются оси инерции. В этом случае:

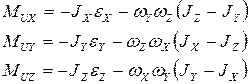
Рассмотрим силовой расчет манипулятора 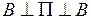. Находим силы инерции звеньев и транспортируемой детали:

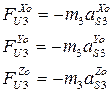
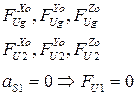
Определяем моменты сил инерции звеньев:

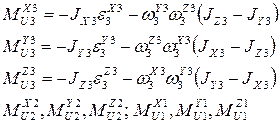
Расчет начинаем с последнего звена “3”. Рисуем его расчетную схему.

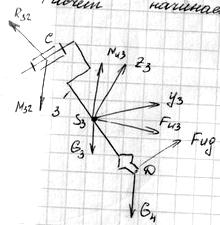
Уравнение сил:

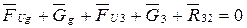
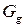- сила тяжести детали.

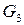- сила тяжести звена “3”.

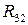- неизвестная реакция звена “3” со стороны звена “2”.

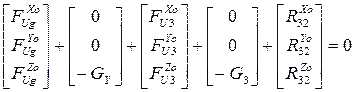
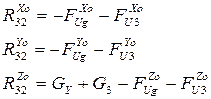
Уравнение равновесия моментов относительно точки “C”:

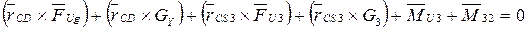
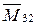- неизвестный реактивный момент, действующий на звено “3” со стороны звена “2”. Находим :

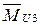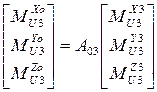
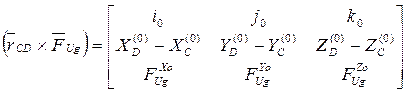
В результате векторное уравнение моментов приводится к трем скалярным уравнениям, из которых определяется :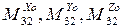

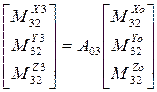
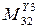- движущий момент во вращательной паре “C”.

Известными являются .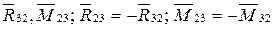

Из уравнения равновесия определяется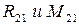

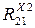- движущая сила в поступательной паре “B”.

Последним рассматривается звено “1”:

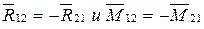
Из уравнения равновесия определяется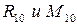

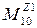- движущий момент во вращательной паре “A”.

Основная теорема зацепления.

Взаимодействующие поверхности звеньев высшей пары, обеспечивающие заданный закон их относительного движения должны быть выполнены так, что бы общая нормаль к ним в любой точке контакта была перпендикулярна вектору относительной скорости:

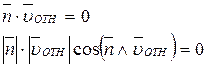
Если условия теоремы не выполняются, то появится составляющая 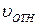на нормаль, что вызовет отрыв или внедрение поверхностей, что исключается.

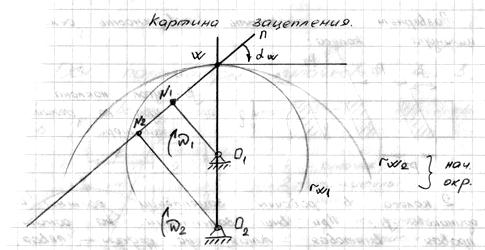
Рассмотрим плоское зацепление:

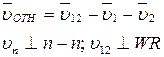
W – мгновенный центр скоростей или полюс зацепления.

n – n – походит через полюс зацепления.

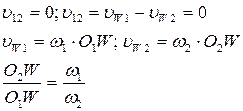
Основная теорема плоского сцепления.

(Теорема Виллиса).

Проекции звеньев высшей пары, передающей вращение между параллельными осями с заданным отношением угловых скоростей, должны быть выполнены так, что бы общая нормаль к ним в точке контакта делила межосевое расстояние на части, обратно пропорциональные угловым скоростям.

Следствия:

1) При 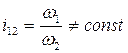полюс зацепления перемещается по межосевой линии.

2) При 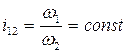полюс зацепления является неподвижной точкой и определяется радиусами 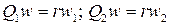, которые перемещаются одна по другой без скольжения и называются начальными.

Эвольвента окружности.

Def: эвольвентой окружности называется траектория общей точки прямой линии, перекатывающейся без скольжения по окружности. Эта окружность называется основной.

Условие переката без скольжения - .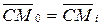

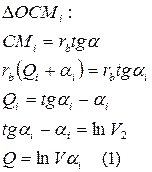
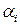- угол продолжения эвольвенты в точке “M”.

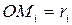- радиус – вектор в точке “M”.

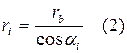
(1) и (2) - уравнения эвольвенты в параметрической форме.

Свойства эвольвенты вытекают из условия образования:

Эвольвента начинается на основной окружности и делит правую и левую ветви. Нормаль в эвольвенте любой ее точке касается основной окружности, а точка касания – есть центр кривизны эвольвенты.

Две эвольвенты одной и той же основной окружности являются эквидистсентными.

При 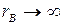эвольвента обращается в прямую линию.

Основные геометрические характеристики зубчатых колес.

Рассмотрим торцовое сечение цилиндрического зубчатого колеса с внешними зубями.

Профиль зуба состоит из эвольвентной части и переходной кривой. Их общая точка 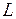- граничная точка профиля.

Окружной шар зубьев – расстояние между одноименными профилями соседних зубьев по дуге окружности. Для окружности произвольного радиуса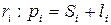

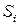- толщина зуба.

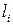- ширина впадины.

Длину произвольной окружности можно выразить двояко:

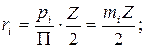
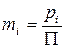- модуль зубьев на окружности.

Шаг 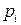и модуль 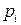зависят от того, к какой окружности они относятся.

Делительная окружность – окружность, на которой модуль зубьев стандартному модулю зуборезного инструмента.

Модуль зубьев разделительной окружности называется расчетным модулем колеса.

Радиус делительной окружности: .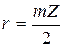

На основании уравнения эвольвенты: .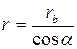

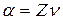- угол профиля на делительной окружности .

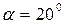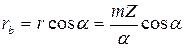
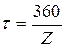- угловой шаг зубьев.

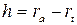- высота зуба.

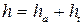
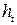- высота делительной ножки зуба.

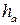- высота делительной головки зуба.

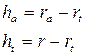
Основные свойства и характеристики эвольвентного зацепления.

Рассмотрим внешнее зацепление эвольвентных профилей.

Первое свойство:

Эвольвентное зацепление обеспечивает передаточное отношение.

Линия зацепления – траектория общей точки контекста “K” профилей.

Второе свойство:

В эвольвентном зацеплении линией зацепления является прямая “n-n” – общая касательная к основным окружностям.

Угол зацепления – угол 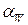между линией зацепления и перпендикуляром к межосевой линии.

Активная линия зацепления – участок 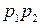линии зацепления, заключенный между окружностями вершин.

Эвольвентные профили касаются только на этом участке.

В контакте участвуют только активные профили .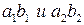

Третье свойство:

При внешнем зацеплении эвольвентные профили могут касаться только в пределах отрезка 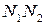, поэтому активная линия 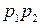не должна выходить за предельные точки 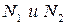, так как там эвольвенты не имеют общей нормали и пересекаются (интерференция эвольвент).

Из 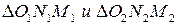связь между радиусами начальных и основных окружностей:

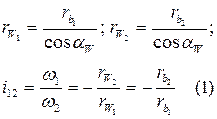
Межосевое расстояние:

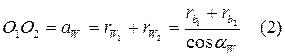
Так как радиусы 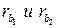являются неизменными из (1) и (2) вытекает:

Четвертое свойство:

При изменении межосевого расстояния в эвольвентном зацеплении передаточное отношение не изменяется, но изменяется угол зацепления 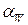и радиусы начальных окружностей, так что 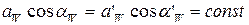, где 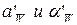- новые значения.

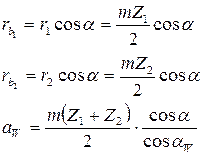
Между окружностями вершин одного колеса и окружностью впадин другого должен быть радиальный зазор “C”. Обычно 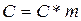, где 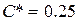- стандартный коэффициент радиального зазора.

Тогда радиусы вершин зубьев:

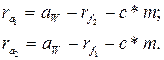
Качественные показатели зацепления.

1) Угол перекрытия.

Угол перекрытия – угол поворота колеса за время зацепления одной пары зубьев.

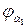- для первого колеса.

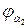- для второго колеса.

Коэффициент перекрытия:

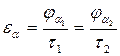- отношение угла перекрытия к угловому шагу зубьев.

Необходимо 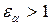. В этом случае следующая пара зубьев входит в зацепление в точке 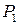еще до того, как предыдущая пара выходит из зацепления в точке .

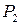Коэффициент перекрытия является показателем непрерывности и плавности зацепления.

Стандарт (требует) рекомендует:

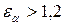- для прямозубых колес.

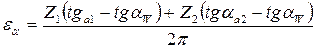
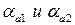- углы профиля эвольвент на окружностях вершин.

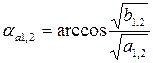
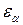- возрастает с увеличением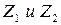

- убывает с увеличением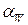

- не зависит от модуля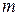

2) Удельное скольжение зубьев.

В данной точке контакта отношение скорости скольжения к скорости перемещения точки контакта по профилю.

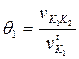- для первого контакта.

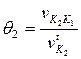- для второго контакта.

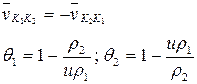
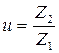- передаточное число.

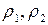- радиусы кривизны эвольвент в точке касания “K”.

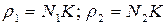
Эпюра удельных скольжений по высоте зуба имеет вид:

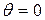- начальные окружности перекатываются без скольжения.

3) Приведенный радиус кривизны профилей в полюсе зацепления.

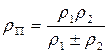
“+” – для внешнего зацепления.

“ - ” – для внутреннего зацепления.

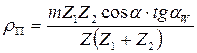
Исходный производящий контур цилиндрических эвольвентных колес.

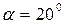- угол главного профиля.

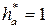- коэффициент высоты головки зуба

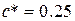- коэффициент радиального зазора.

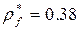- коэффициент радиуса кривизны переходной кривой.

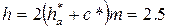
Граничные прямые определяют скругления от прямых участков.

По делительной прямой ширина зуба равна ширине впадины.

Колеса без смещения о со смещением исходного контура.

Если делительная прямая касается делительной окружности нарезаемого колеса, то нарезается колесо без смещения, в противном случае нарезается колесо со смещением.

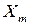- смещение исходного контура.

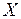- коэффициент смещения.

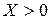- делительная прямая не пересекает делительную окружность – смещение положительно.

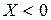- делительная прямая пересекает делительную окружность – смещение отрицательно.

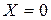- колеса без смещения.

В процессе нарезания начальная прямая и делительная окружность перекатывается друг по другу, поэтому толщина зуба колеса по делительной окружности равна ширине впадины 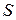по начальной прямой.

Для колеса без смещения:

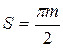
В общем случае:

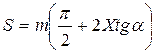
Станочное зацепление нарезаемого колеса с реечным инструментом.

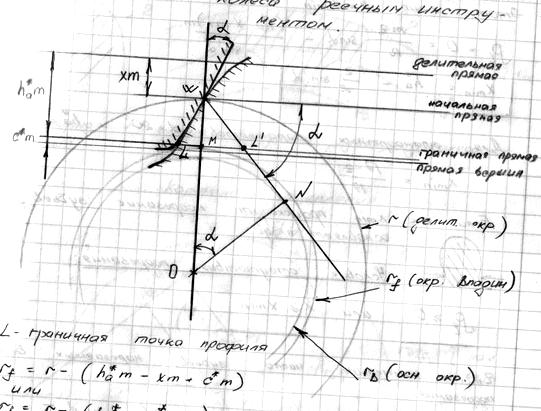
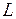- граничная точка профиля.

Из рисунка:

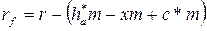
или:

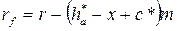
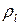- радиус кривизны граничной точки (эвольвенты в граничной точке)

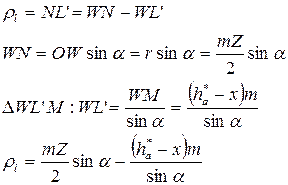
Подрезание зубьев.

Из формулы 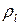видно, что для каждого 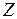существует такой коэффициент 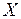, при котором 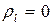, то есть граничная точка 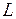будет лежать на основании окружности 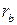. Этот коэффициент 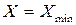- коэффициент наименьшего смещения.

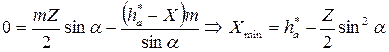
Для стандартных параметров :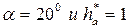

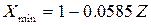или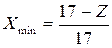

Если 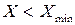, происходит подрезание зубьев – срезание части эвольвентного профиля. Это ослабляет зуб и недопустимо.

Условие отсутствия подрезания:

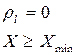
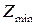- наименьшее число зубьев, нарезанных без подрезания.

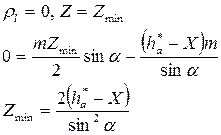
Для стандартных параметров 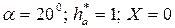- без смещения.

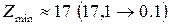- незначительное подрезание.

Путем соответствующего выбора коэффициентов 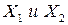можно:

1) Устранять подрезание при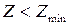

2) Повышать контактную и изгибную прочность зубьев.

3) Получать заданное межосевое расстояние.

Особенности внутреннего зацепления.

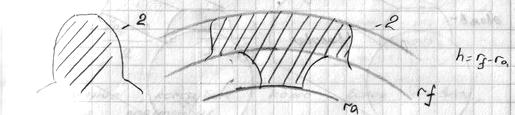
Шестерня “1” имеет выпуклые зубья, а колесо “2” – вогнутые.

Касание эвольвент возможно только за пределами отрезка .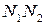

Колеса с внутренними зубьями нарезаются долбяком – колесо с зубьями эвольвентного профиля.

Межосевое расстояние:

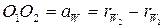
Преимущества внутреннего зацепления:

1) Более высокая контактная прочность, так как в контакте находятся выпуклый и вогнутый профиль.

2) Меньшее скольжение зубьев меньший износ.