Звено приведения:
Разгон:
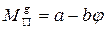 - прямая линия
- прямая линия
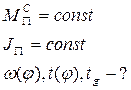
Решение.
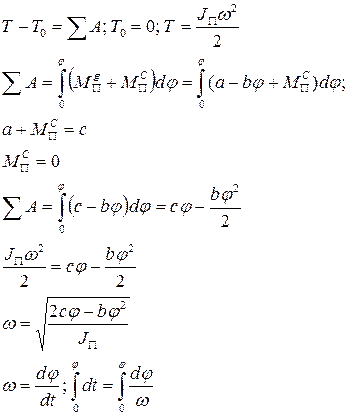
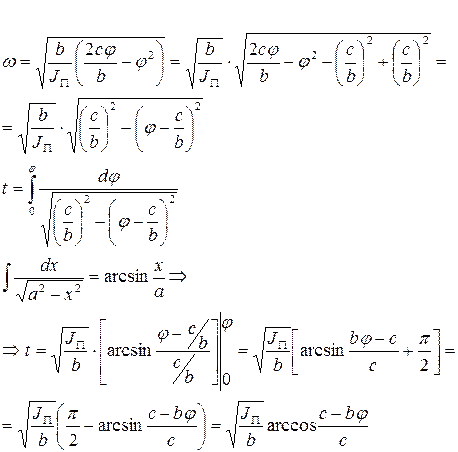
При 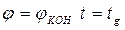 - время разгона.
- время разгона.
Задача ограничения периодических колебаний скорости.
Периодические колебания скорости звена приведения при установившемся движении вызываются двумя основными причинами:
1) Несовпадение законов изменения 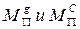 (силовое возмущение).
(силовое возмущение).
2) 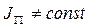 - переменный характер приведенного момента инерции – инерционное возмущение.
- переменный характер приведенного момента инерции – инерционное возмущение.
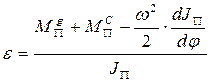 (1)
(1)
Равномерное движение 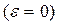 возможно, если:
возможно, если:
1) 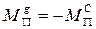
2) 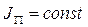
Колебания скорости вызывают переменные нагрузки в кинематических парах, что отрицательно влияет на технологический процесс, поэтому они допускаются лишь в определенных пределах.
Вводится коэффициент неравномерности движения:
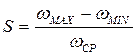 (2)
(2)
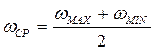 (3)
(3)
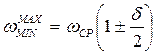
Одним из способов обеспечить заданный коэффициент неравномерности движения является увеличение инерционности машины путем установки дополнительной маховой массы (маховика).
Из формулы (1) видно, что чем больше 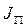 , тем меньше
, тем меньше 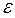 . Увеличивая массу, увеличиваем
. Увеличивая массу, увеличиваем 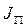 , уменьшаем
, уменьшаем 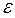 .
.
Определение постоянной составляющей 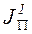 приведенного момента инерции машины по заданному коэффициенту неравномерности движения.
приведенного момента инерции машины по заданному коэффициенту неравномерности движения.
|
|
|
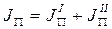
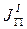 - постоянное слагаемое.
- постоянное слагаемое. 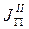 - переменное слагаемое.
- переменное слагаемое.
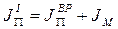
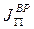 - приведенный момент вращающихся звеньев.
- приведенный момент вращающихся звеньев. 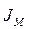 - искомый момент инерции маховика.
- искомый момент инерции маховика.
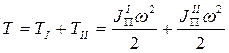
Пусть при 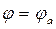 имеем
имеем 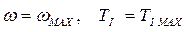
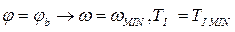
Тогда находим наибольший перепад:
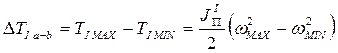
Учитывая, что 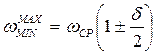 , имеем:
, имеем:
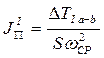 (1)
(1)
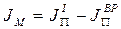 (2)
(2)
Общий случай.
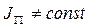 Метод Н.И. Мерцалова.
Метод Н.И. Мерцалова.
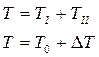
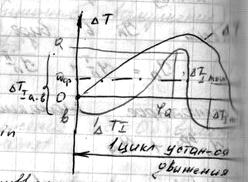
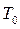 - кинетическая энергия в начале цикла.
- кинетическая энергия в начале цикла.
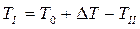
Так как неизвестная величина 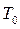 не влияет на характер графика, то достаточно построить график
не влияет на характер графика, то достаточно построить график 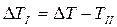
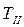 определяется приближенно по средней угловой скорости:
определяется приближенно по средней угловой скорости:
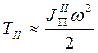
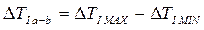
Используем формулы (1) и (2):
График 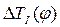 одновременно является приближением графика
одновременно является приближением графика 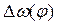
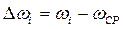
Линия 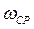 проходит посередине отрезка “ab”
проходит посередине отрезка “ab”
Масштабный коэффициент:
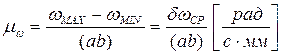
2) Частный случай 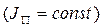
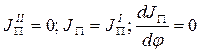
В точках экстремума 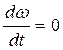 , тогда дифференциальное уравнение:
, тогда дифференциальное уравнение:
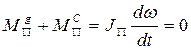
Следовательно, положение 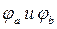 определяется точками пересечения графиков
определяется точками пересечения графиков
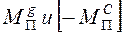 .
.
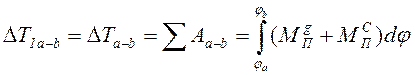
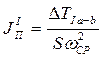 (1)
(1)
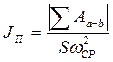
Пример.
Для машины с синусным механизмом определить момент инерции маховика 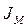
Движущий момент 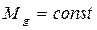 (принять постоянным). Сила сопротивления
(принять постоянным). Сила сопротивления 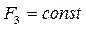 (постоянная) и действует в интервале
(постоянная) и действует в интервале 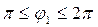 . Переменной составляющей пренебречь.
. Переменной составляющей пренебречь.
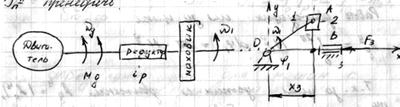
Решение.
Кинематические характеристики:
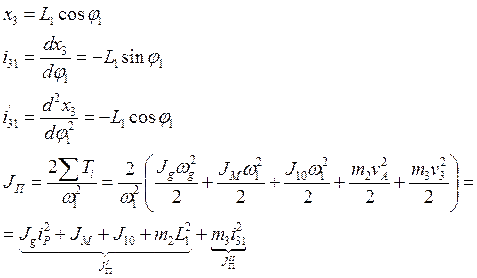
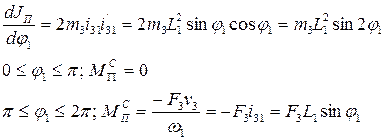
Работа сил сопротивления за цикл:
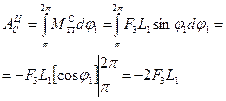
Работа движущих сил за цикл:
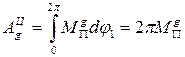
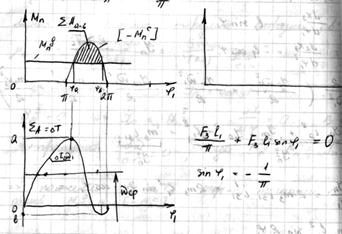
Так как за цикл установившегося движения 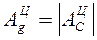 , то, приравняв, имеем:
, то, приравняв, имеем:
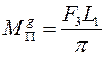
Находим 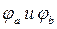 углы:
углы:
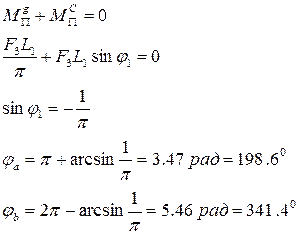
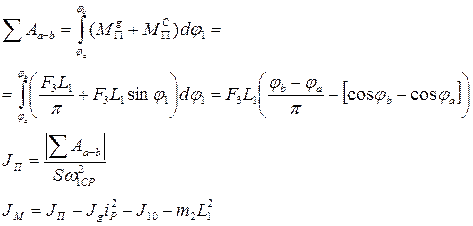
Определение 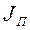 для машины с электроприводом.
для машины с электроприводом.
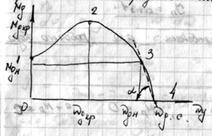 Рассмотрим механическую характеристику трехфазного асинхронного электродвигателя переменного тока.
Рассмотрим механическую характеристику трехфазного асинхронного электродвигателя переменного тока.
1 – пуск двигателя
2 – критические значения 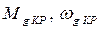
3 – номинальные значения 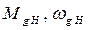
4 – холостой ход 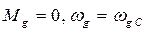 - синхронная скорость.
- синхронная скорость.
2 – 3 – 4 – зона устойчивой работы двигателя.
1 – 2 – зона неустойчивой работы - при выходе на нее двигатель останавливается (опрокидывается).
|
|
|
Устойчивый участок приближенно можно описать в виде прямой линии, проходящей через точки 3 – 4.
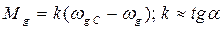
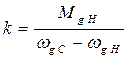 - крутизна (жесткость) характеристики.
- крутизна (жесткость) характеристики.
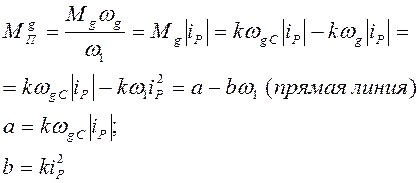
Рассмотрим случай, характерный для машин ударного действия.
Холостой ход – от ωmin до ωmax
Рабочий ход – от ωmax до ωmin
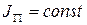
Дифференциальное уравнение движения для рабочего хода:
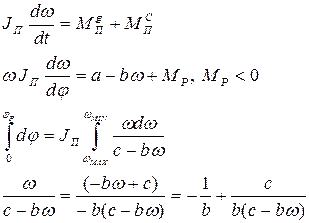
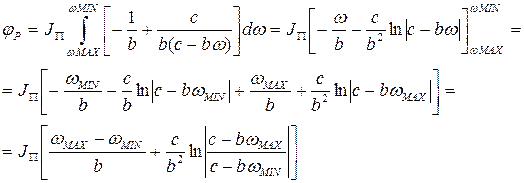
Отсюда:
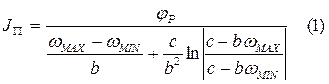
Составляем дифференциальное уравнение движения для холостого хода:
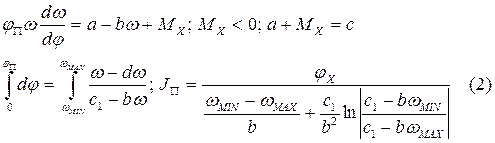
В (1) и (2) три неизвестных: 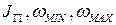
Задавая 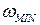 , можно найти
, можно найти 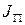 и
и 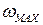
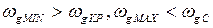
Учет динамической характеристики двигателя.
Характеристика 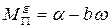 является статической, так как не учитывает инерционности процессов, связанных с изменением нагрузки во времени.
является статической, так как не учитывает инерционности процессов, связанных с изменением нагрузки во времени.
Для учета этих процессов используется динамическая характеристика в виде:
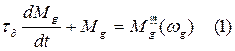
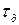 - электромагнитная составляющая времени.
- электромагнитная составляющая времени.
Переходим к звену приведения.
Уравнение (1) запишем в следующем виде:
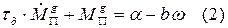
Вместе с уравнением (2) рассматриваем уравнение движения звена приведения, которое при 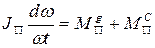
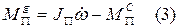
Продифференцируем:
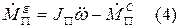
Уравнения (3) и (4) подставим в уравнение (2), учитывая электромагнитную инерцию:
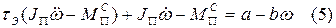
Используем уравнение (5) для определения зависимости 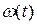 при разгоне машины в случае
при разгоне машины в случае 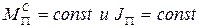 :
:
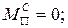
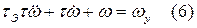 , где:
, где:
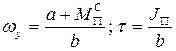 - постоянна.
- постоянна.
Составляем характеристическое уравнение:
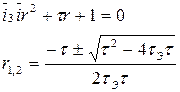
1) 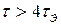 - корни действительные, различные и отрицательные.
- корни действительные, различные и отрицательные.
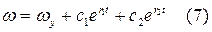
При 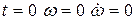 :
:
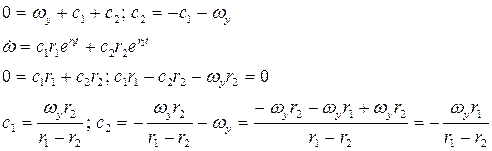
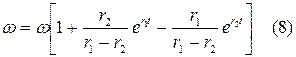
Уравнение (8) описывает апериодический процесс.
При 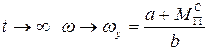 - угловая скорость установившегося движения.
- угловая скорость установившегося движения.
2) 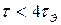 Корни
Корни 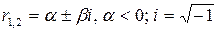
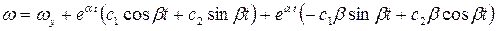
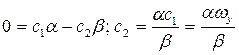
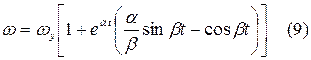
Затухающий процесс.
Такой режим разгона допускать не следует!
Если решать рассматриваемую задачу, исходя из статической характеристики, т.е. при 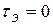 , то выявить колебания при разгоне не удастся. Для этого случая было ранее получено:
, то выявить колебания при разгоне не удастся. Для этого случая было ранее получено:
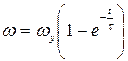
3) 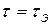
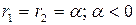
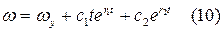
Уравнение (10) описывает апериодический неколебательный процесс.
Лекция.
Метод кинетостатики. Силы инерции звеньев.
Силовой анализ механизма выполняется методом кинетостатики, который состоит в том, что уравнения движения записываются в форме уравнений равновесия или статики. Для этого к каждому подвижному звену механизма наряду с реально действующими активными силами и реакциями связи прикладываются силы инерции, после чего, на основании принципа Даламбера, составляются уравнения равновесия в следующем виде:
1) Векторная сумма всех сил равна нулю. 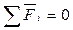 или
или 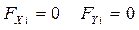
2) Сумма моментов 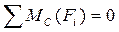
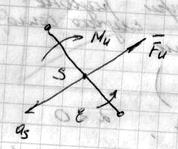 Силы инерции звена, совершающего плоскопараллельное движение и имеющего плоскость симметрии, параллельную плоскости движения, приводятся к главному вектору
Силы инерции звена, совершающего плоскопараллельное движение и имеющего плоскость симметрии, параллельную плоскости движения, приводятся к главному вектору 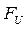 , приложенному в центре масс “S” и главному моменту
, приложенному в центре масс “S” и главному моменту 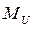 :
:
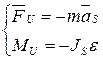
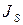 - центральный момент инерции.
- центральный момент инерции.
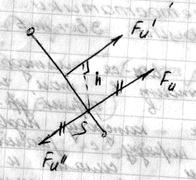 Силу
Силу 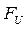 и момент
и момент 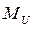 можно заменить одной силой
можно заменить одной силой 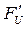 , приложенной на расстоянии “H” от “S”:
, приложенной на расстоянии “H” от “S”:
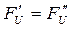 - пара сил
- пара сил
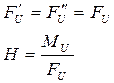
Рассмотрим частные случаи.
1) Поступательное движение звена.

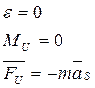
2) Вращательное движение звена вокруг оси, проходящей через центр масс.
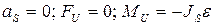
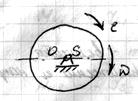
3) Вращательное движение вокруг оси, не проходящей через центр масс:
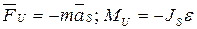
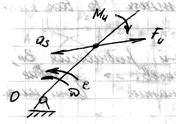
Условия статической определимости плоских кинематических цепей.
Рассмотрим действия реакций в различных кинематических парах без учета трения.
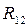 - реакция на звено “1” со стороны звена “2”
- реакция на звено “1” со стороны звена “2”
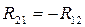
Условия статической определимости плоских кинематических цепей.
Рассмотрим действие реакций в различных кинематических парах без учета трения:
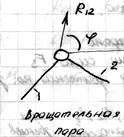
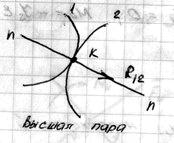
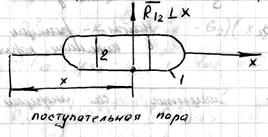
1) Вращательная пара. 2) Поступательная пара. 3) Высшая пара.
R12 – реакция на звено 1
 со стороны звена 2.
со стороны звена 2. 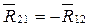
Во вращательной паре неизвестны величина и направление реакций, а точка приложения известна (центр шарнира) – неизвестна.
В поступательной паре неизвестны величина и точка приложения, а направление известно.
В высшей паре неизвестна величина, а точка приложения и направление известны.
Таким образом, общее число неизвестных равно: 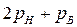 .
.
Общее число возможных уравнений равновесия: 3n,n – число подвижных звеньев.
Следовательно, условие статической определимости в кинематической цепи имеет вид: 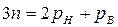
Для рычажных механизмов pB = 0, тогда условие: 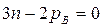
|
|
|
Этому условию удовлетворяют структурные группы (группы Ассура).
Кинетостатический силовой анализ плоских рычажных механизмов аналитическим методом.
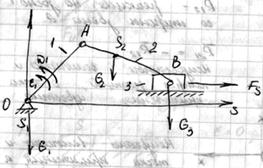 Пример.
Пример.
Задано:
Закон движения начального звена 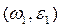
Внешняя сила: 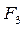
Силы тяжести звеньев: 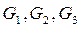
Определить:
Реакции в кинематических парах
(взаимодействие между звеньями)
Решение.
Определяем силы и моменты сил инерции:
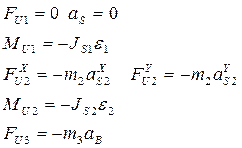
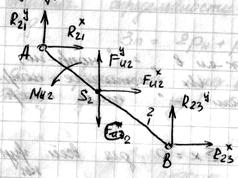
Отделяем от механизма статически определимую структурную группу (2,3):
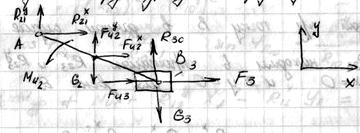 Силы и моменты показываем в положительном
Силы и моменты показываем в положительном
положении кроме сил тяжести.
Их истинное направление укажет знак “+”
или “-” после числовых расчетов.
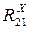 находим из уравнения:
находим из уравнения:
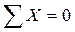 для всей группы.
для всей группы.
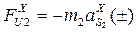
Составляем сумму проекций на ось Х:
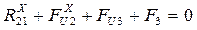
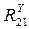 находим из уравнения:
находим из уравнения:
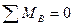 для звена “2”.
для звена “2”.
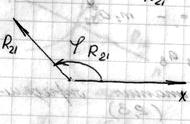
 находим из уравнения:
находим из уравнения:
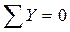 - для всей группы.
- для всей группы.
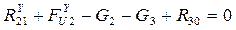
В данном случае 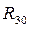 проходит через т. В.
проходит через т. В.
Реакцию 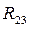 находим в проекциях
находим в проекциях 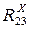 и
и 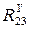 из уравнений:
из уравнений:
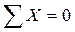 и
и 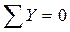 - для звена “2”.
- для звена “2”.
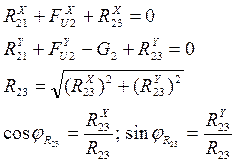
Рассчитаем начальное звено “1”:
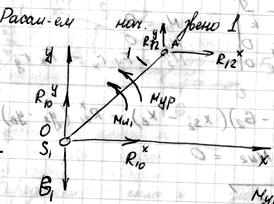
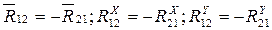
Мур – уравновешивающий (движущий) момент, который действует со стороны привода и обеспечивает принятый закон движения.
Имеем:
Статически определимая задача:
Три неизвестных - 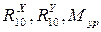
Три уравнения равновесия.
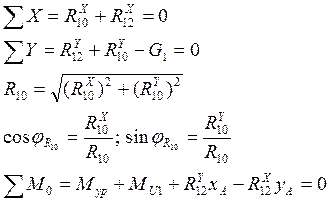
Трение.
По характеру относительно движения различают следующие виды трения:
1) Трение скольжения.
2) Трение качения.
3) Трение верчения (частный случай трения качения).
В зависимости от состояния, взаимодействующих тел:
1) Сухое трение.
2) Трение со смазывающим материалом.
3) Переходные (промежуточные) виды.
Рассмотрим основные закономерности трения скольжения:
RH – нормальная реакция.
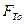 - касательная реакция (сила трения покоя {сцепления})
- касательная реакция (сила трения покоя {сцепления})
Fg – движущая сила.
В момент трогания с места:
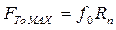
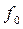 - коэффициент трения покоя (сцепления).
- коэффициент трения покоя (сцепления).
Когда:
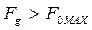 - скольжение.
- скольжение.
FT – сила трения скольжения, направлена против 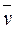
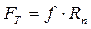
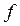 - коэффициент трения скольжения.
- коэффициент трения скольжения.
Для конкретных материалов 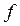 - постоянен.
- постоянен.
Экспериментальные исследования показывают, что:
1) С увеличением относительной скорости коэффициент трения в большинстве случаев уменьшается, приближаясь к некоторому постоянному значению.
2) С увеличением давления коэффициент трения в большинстве случаев увеличивается.
|
|
|
3) С увеличением времени предварительного контакта коэффициент трения возрастает.
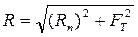 - полная реакция отклоняется на угол φ от нормали.
- полная реакция отклоняется на угол φ от нормали.
φ – угол трения.
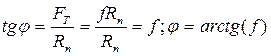
Угол трения покоя:
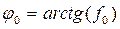
Конус трения.
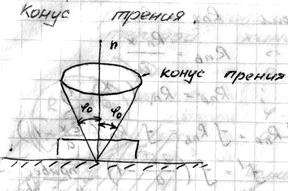 Конус трения ограничивает область равновесия тела (любая сила F, приложенная к телу под углом
Конус трения ограничивает область равновесия тела (любая сила F, приложенная к телу под углом 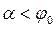 , не может привести его в движение).
, не может привести его в движение).
F’ – движущая сила
F’’ – нормальное давление
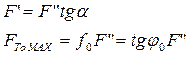
Если 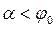 , то
, то 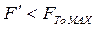 и движение невозможно.
и движение невозможно.
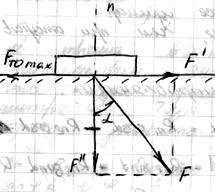
Трение скольжения в
поступательной паре.
1) Трение на одной плоскости. 2) Трение по двум плоскостям
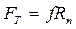 (перекос ползуна).
(перекос ползуна). 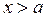
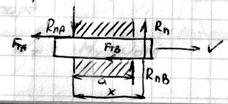
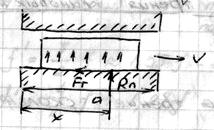
Rn – приложена не в зоне контакта и является равнодействующей двух параллельных сил
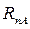 и
и 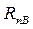
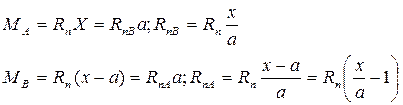
Суммарная сила трения:
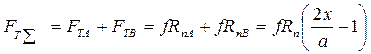
Или:
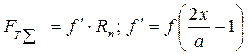 - приведенный коэффициент трения.
- приведенный коэффициент трения.
Так как 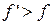 , то при переносе суммарная сила трения больше, чем при отсутствии перекоса.
, то при переносе суммарная сила трения больше, чем при отсутствии перекоса.
3) Трение в клиновых направляющих.
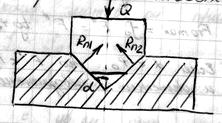
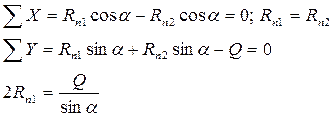
Суммарная сила трения:
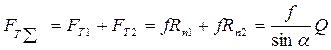
или:
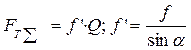 - приведенный коэффициент трения.
- приведенный коэффициент трения.
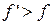
Потери мощности на трение скольжения:
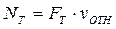
 Трение скольжения во вращательной кинематической паре.
Трение скольжения во вращательной кинематической паре.
а – радиус круга трения.
Полная реакция “R” касается круга трения радиуса “a”.
Он имеет тот же смысл, что и конус трения в поступательной паре.
При силовом анализе удобнее считать, что полная реакция “R”
проходит через центр “O”. Тогда для учета трения надо
добавить момент трения.

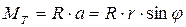 .
.
Для малых углов 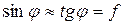 , тогда:
, тогда:
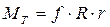
Реально коэффициент трения 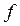 между цилиндрическими поверхностями больше, чем между плоскими.
между цилиндрическими поверхностями больше, чем между плоскими.
Поэтому:
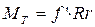 ,
, 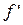 - приведенный коэффициент трения во вращательной паре.
- приведенный коэффициент трения во вращательной паре.
1) 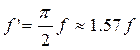 - для новых неприработавшихся пар.
- для новых неприработавшихся пар.
2) 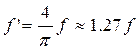 - для приработавшихся пар.
- для приработавшихся пар.
Потери мощности на трение во вращательной паре:
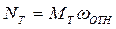
Трение качения в высших кинематических парах.
Покой:
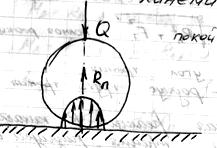
В высших кинематических парах происходит трение качения или одновременно качение со скольжением.
Перекатывание:
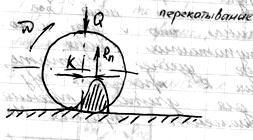
Rn – смещается на величину “k” – коэффициент трения качения.
1) При качении стальных колес по стальным рельсам – k = 0.05 мм.
2) Качение автомобильных шин по сухому асфальту – k = 2.5 мм.
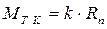
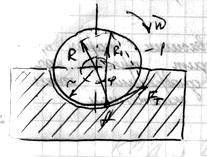
Рассмотрим задачу о перекатывании цилиндра движущей силой 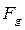 :
:
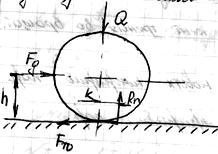
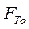 - сила трения покоя (сцепления)
- сила трения покоя (сцепления)
При равномерном движении:
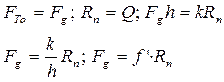
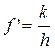 - приведенный коэффициент трения.
- приведенный коэффициент трения.
Чтобы качение сопровождалось скольжением, необходимо, что бы 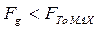
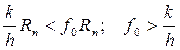 - условие чистого качения.
- условие чистого качения.
Потери мощности на трение качения.
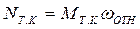
Коэффициент полезного действия (КПД) и коэффициент потерь.
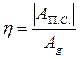 - цикловой КПД.
- цикловой КПД.
АП.С. – работа сил полезного сопротивления;
Аg – работа движущих сил.
За цикл:
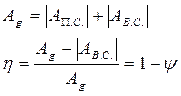
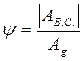 - коэффициент потерь.
- коэффициент потерь.
АВ.С. – работа сил вредного сопротивления.
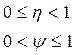
Вместо работ можно брать средние мощности:
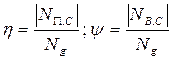
Иногда определяется мгновенный КПД:
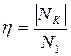
N1 – мощность на ведущем звене.
NK – мощность на ведомом звене.
Эти мощности определяются без учета сил инерции.
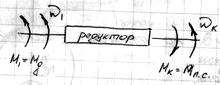 Для механизмов передач вращательного движения (редуктор) цикловой и мгновенный КПД совпадают.
Для механизмов передач вращательного движения (редуктор) цикловой и мгновенный КПД совпадают.
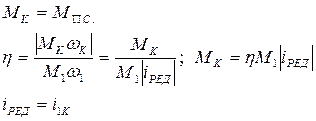
Мгновенный КПД можно представить:
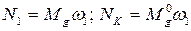
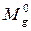 - движущий момент, определяемый без учета трения.
- движущий момент, определяемый без учета трения.
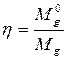 - отношение движущего момента в идеальном механизме и движущего момента в реальном механизме.
- отношение движущего момента в идеальном механизме и движущего момента в реальном механизме.
При прямолинейном движении:
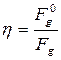
КПД при последовательном и параллельном соединении механизмов.
1) Последовательное соединение:
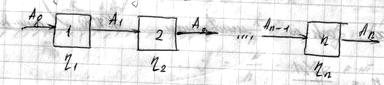
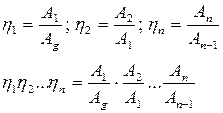
Но 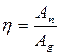 - общий КПД.
- общий КПД. 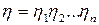 - общий КПД.
- общий КПД.
Общий КПД всегда меньше самого низкого КПД одного механизма.
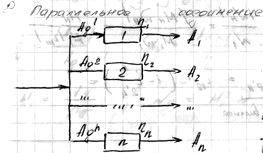
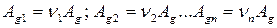
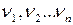 - коэффициенты распределения энергии.
- коэффициенты распределения энергии.
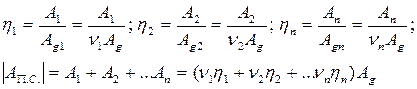
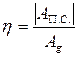 или
или 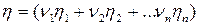
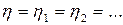 - общий КПД равен КПД каждого механизма.
- общий КПД равен КПД каждого механизма.
Пример 1.
Комбинированный зубчатый механизм.
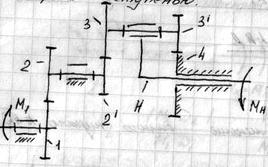
1 – 2 – простая ступень.
2’ – 3 – 3’ – 4 – H – планетарная ступень.
Определить движущий момент 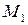 для преодоления момента полезного сопротивления
для преодоления момента полезного сопротивления 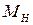 , если заданы КПД отдельных ступеней
, если заданы КПД отдельных ступеней 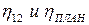 .
.
Решение.
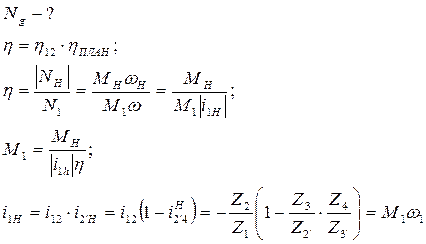
Пример 2.
При установившемся движении сила полезного сопротивления 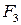 действует при движении ползуна “3” слева направо и изменяется по закону
действует при движении ползуна “3” слева направо и изменяется по закону 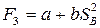 .
.
Определить постоянный движущий момент 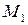 и мощность движущих сил
и мощность движущих сил 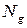 , если задан КПД всего механизма
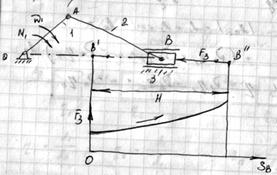
, если задан КПД всего механизма 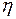 .
.
Решение.
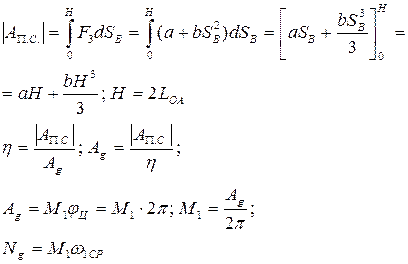
КПД передачи “Винт - гайка”.
Передачу “винт - гайка” приближенно можно представить в виде ползуна, движущегося по наклонной плоскости, которая получается путем развертки средней винтовой линии резьбы на плоскость.
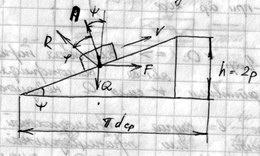
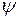 - угол наклона средней винтовой линии.
- угол наклона средней винтовой линии.
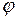 - угол трения.
- угол трения.
h – ход винтовой линии.
p – шаг резьбы.
z – число заходов.
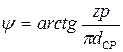 ;
;
При прямом ходе винт преодолевает осевую нагрузку 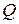 :
:
F – движущая сила.
R – полная реакция.
При равномерном движении:
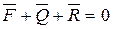
Силовой треугольник:
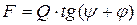
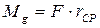 или
или 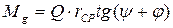
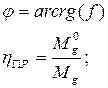
При 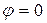
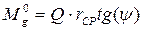
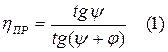 - КПД при прямом ходе.
- КПД при прямом ходе.
При обратном ходе винт движется под действием осевой силы 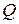 (опускание ползуна)
(опускание ползуна)
F – тормозящая сила, необходимая для равномерного опускания.
Силы трения изменяют свое направление на противоположное:
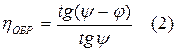 - КПД при обратном ходе.
- КПД при обратном ходе.
Если 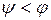 , то получается, что КПД при обратном ходе
, то получается, что КПД при обратном ходе 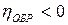 - винтовая пара является самотормозящей – движение под действием любой силы
- винтовая пара является самотормозящей – движение под действием любой силы 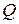 невозможно.
невозможно.
Формулы (1) и (2) используются в случае прямоугольной резьбы.
При треугольной или трапецеидальной резьбе полагают, что движение гайки аналогично движению клинового ползуна.
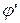 - приведенный угол трения.
- приведенный угол трения.

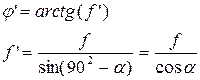
Метрическая резьба 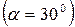 :
:
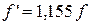
Формулы (1) и (1) используются и для червячной передачи. При передаче движения от червяка на колесо:
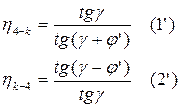
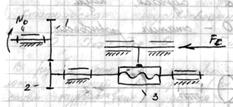
Пример:
Определить движущий момент 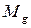 для преодоления силы сопротивления
для преодоления силы сопротивления 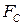 , приложенной к поступательно перемещающейся гайке “3”. Резьба – прямоугольная.
, приложенной к поступательно перемещающейся гайке “3”. Резьба – прямоугольная.
Решение.
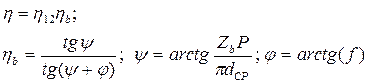
С другой стороны общий КПД:
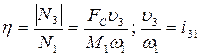 - передаточная функция механизма.
- передаточная функция механизма.
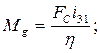
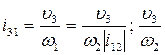 - передаточная функция винтовой пары.
- передаточная функция винтовой пары.
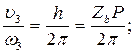
Таким образом:
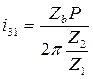
Уравновешивание вращающихся масс.
Уравновешивание масс состоит в устранении переменных реакций на опоры от сил инерции.
Для полного устранения этих реакций главный вектор и главный момент инерции должны быть равны нулю.
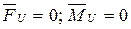 - динамическое уравновешивание.
- динамическое уравновешивание.
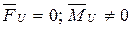 - статическое уравновешивание.
- статическое уравновешивание.
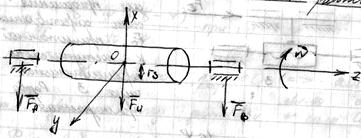
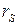 - смещение центра масс “S” относительно оси вращения.
- смещение центра масс “S” относительно оси вращения.
При 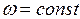 :
:
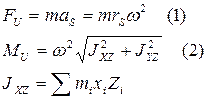
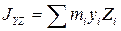 - центральные моменты инерции массы.
- центральные моменты инерции массы.
Из формул (1) и (2) следует, что для динамического уравновешивания должны выполняться два условия:
1) 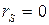
2) 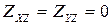
При выполнении этих двух условий ось вращения совпадает с одной из главных центральных осей инерции тела.
Рассмотрим различные виды неуравновешенности:
1) Статическая неуравновешенность:
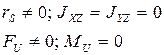
В результате:
Мерой статической неуравновешенности является дисбаланс:
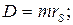
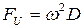 (при
(при 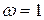 дисбаланс – сила инерции)
дисбаланс – сила инерции)
Пример:
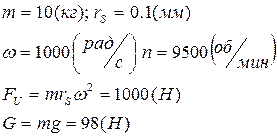
Опоры будут нагружены в десятки раз больше веса:
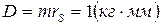
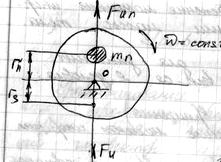 Для устранения статической неуравновешенности надо в направлении, противоположном центру масс поместить корректирующий груз (противовес), масса которого
Для устранения статической неуравновешенности надо в направлении, противоположном центру масс поместить корректирующий груз (противовес), масса которого 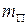 определяется из условия, что:
определяется из условия, что:
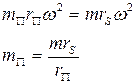
После установки противовеса центр масс “S” сместится на ось вращения
“O”.Часто вместо установки дополнительной массы высверливают
такую же массу с диаметрально противоположной стороны.
Статическое уравновешивание достаточно для узких деталей,
у которых размер вдоль оси вращения мал по сравнению с остальными размерами.
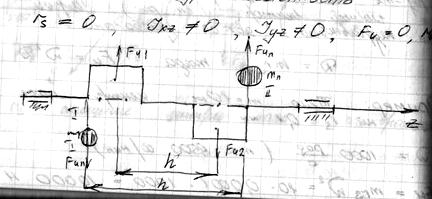
2) Моментная неуравновешенность:
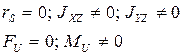
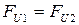 - пара сил с моментами
- пара сил с моментами
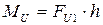
Мерой неуравновешенности служит момент дисбаланса:
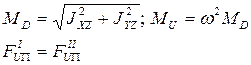
Так как пару сил можно уравновесить только парой сил, то моментная неуравновешенность устраняется двумя одинаковыми противовесами, которые создают момент 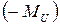 :ъ
:ъ
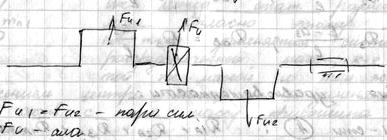
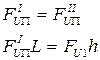
3) Динамическая неуравновешенность:
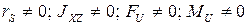
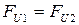 - пара сил
- пара сил
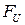 - сила.
- сила.
Динамическую неуравновешенность к двум
статическим в двух плоскостях, поэтому мерой динамической неуравновешенности являются два дисбаланса 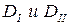 в двух плоскостях.
в двух плоскостях.
Следовательно, динамические неуравновешенности устраняются двумя различными противовесами в двух плоскостях.
Экспериментальное устранение неуравновешенностей называется балансировкой.
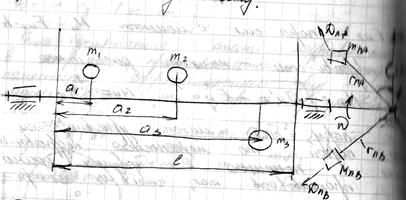 Пример: уравновесить массы
Пример: уравновесить массы 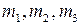 , вращающиеся на одном валу.
, вращающиеся на одном валу.
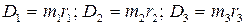
Каждый дисбаланс раскладываем
на 2 параллельных:
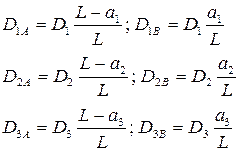
Условие уравновешенности:
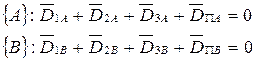
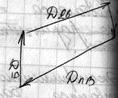 Строим многоугольники дисбалансов:
Строим многоугольники дисбалансов: 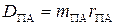
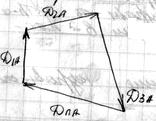
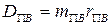
Уравновешивание масс механизмов.
Для механизмов в целом чаще всего ограничиваются статическим уравновешиванием, когда 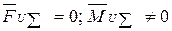
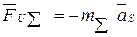
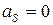 , то есть общий центр масс всего механизма должен быть неподвижным.
, то есть общий центр масс всего механизма должен быть неподвижным.
 Рассмотрим задачу статического уравновешивания масс кривошипно – ползунного механизма:
Рассмотрим задачу статического уравновешивания масс кривошипно – ползунного механизма:
Статическое размещение масс.
Согласно этому методу, твердое тело
заменяется системой сосредоточенных
(точечных) масс, которые обладают той
же массой и тем же расположением
центра масс, что и заменяемое тело.
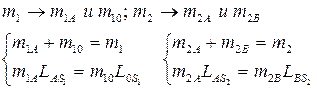
Из этих уравнений находим:
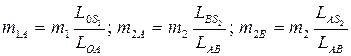
В результате в точке “A” сосредоточена вращающаяся масса: 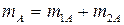
В точке “B” – поступательно движущаяся масса.
На продолжении звена “2” в точке “C” устанавливаем противовес, массу которого 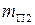 находим из условия, что бы центр масс
находим из условия, что бы центр масс 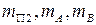 , оказался точке “A”.
, оказался точке “A”.
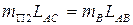
В точке “D” устанавливаем противовес, массу которого находим из условия, что бы центр масс 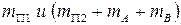 оказался в точке “O”.
оказался в точке “O”.
После установки обоих противовесов общий центр масс общий центр масс механизма окажется в неподвижной точке “O”, где достигается статическое уравновешивание.
Рассмотрение решения является конструктивно неудачным и применяется редко, поэтому часто применяется приближенное статическое уравновешивание, например:
Рассмотрим уравновешивание только вращающихся масс:
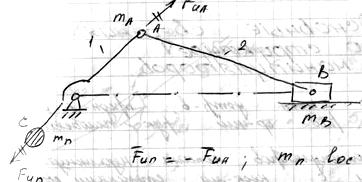
Уравновешивание только вращающихся масс:
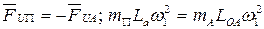
Неуравновешенной остается сила инерции от поступательно движущейся массы 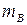 :
:
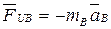
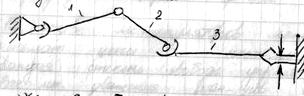
Основные сведения о структуре манипуляторов.
Манипулятор – механическое устройство, предназначенное для воспроизведения рабочих функций рук человека.
В основе манипуляторов незамкнутые кинематические цепи с несколькими степенями свободы.
Каждая степень свободы управляется отдельным приводом.
Все механические движения манипуляторов делятся на:
1) Переносные.
2) Ориентирующие.
Переносные движения обеспечивают перемещение объекта манипулирования в требуемую точку пространства, а ориентирующие движения выполняют его ориентацию нужным способом.
Рабочая зона манипулятора будет объемной (пространственной), если число переносных степеней свободы 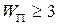 .
.
Число ориентирующих степеней свободы обычно 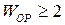 .
.
1) Манипулятор 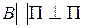
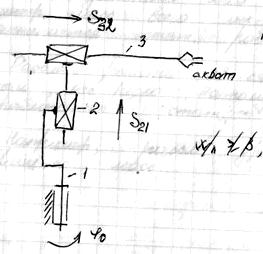
Переносное движение и степени свободы:
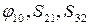
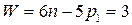 - степени свободы.
- степени свободы.
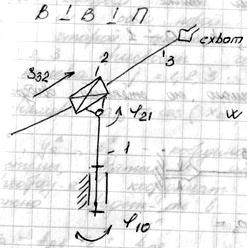 2)
2) 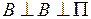 3)
3) 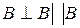
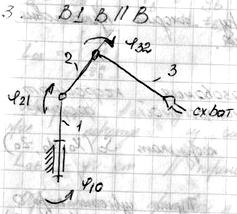
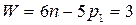
Часть рабочей зоны, в которой рука манипулятора выполняет свои функции, называется зоной обслуживания.
Для каждой точки зоны обслуживания существует такой телесный (пространственный) угол 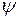 , внутри которого схват может подойти к этой точке.
, внутри которого схват может подойти к этой точке.
 - угол сервиса.
- угол сервиса.
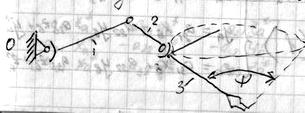
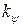 - коэффициент сервиса в данной точке.
- коэффициент сервиса в данной точке.
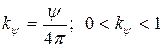
Маневренность манипулятора – число степеней свободы при неподвижном схвате.
Метод преобразования координат в матричной.
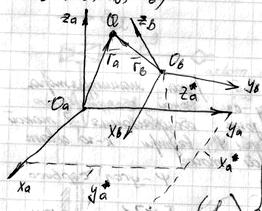 Рассмотрим две системы координат:
Рассмотрим две системы координат:
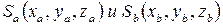
Пусть известны координаты точки “Q” в системе
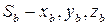 , тогда координаты этой же точки
, тогда координаты этой же точки
в системе 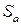 определяются по формуле:
определяются по формуле:
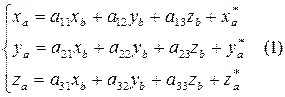
Здесь каждый коэффициент 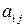 - косинус угла между
- косинус угла между 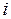 - й осью новой системы
- й осью новой системы 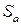 и
и 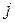 - й осью старой системы
- й осью старой системы 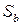 , причем номера
, причем номера 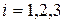 присвоены соответственно осям
присвоены соответственно осям 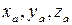 , а номера
, а номера 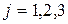 - соответственно осям
- соответственно осям 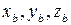 .
.
Например:
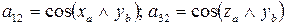
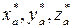 - координаты начала старой системы
- координаты начала старой системы 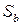 в новой системе
в новой системе 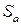 .
.
Преобразование координат точки по формулам (1) можно двумя способами:
1) С помощью матриц третьего порядка.
2) С помощью матриц четвертого порядка.
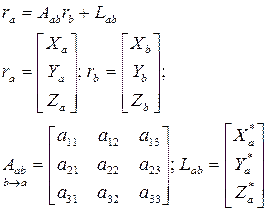
Матрица  учитывает поворот координатных осей из системы “b” в систему “a”.
учитывает поворот координатных осей из системы “b” в систему “a”.
Матрица – столбец учитывает параллельный перенос осей.
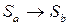 - обратное преобразование.
- обратное преобразование.
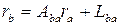
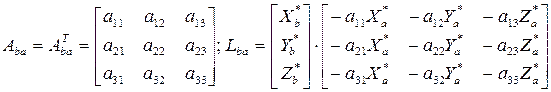
2) 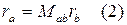
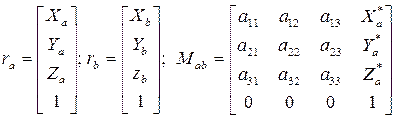
После перемножения матриц по формуле (2) получается выражение (1) и тождество 1 = 1.
Преобразование координат векторов выполняется с помощью матриц поворота 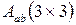 , так как проекции вектора не зависят от параллельного переноса осей.
, так как проекции вектора не зависят от параллельного переноса осей.
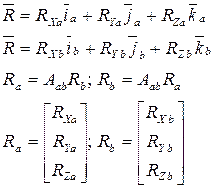
Часто для перехода из системы 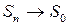 используются промежуточные системы координат
используются промежуточные системы координат 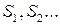
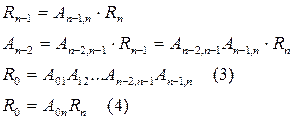
Сравнивая (3) и (4), получаем:
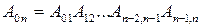
Составим выражения матриц для одноосных поворотов.
1) Поворот вокруг общей оси 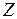 :
:
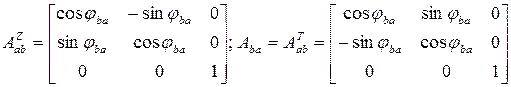
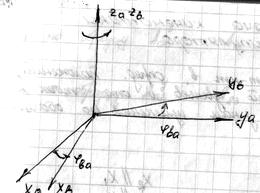 м
м
2) Поворот вокруг общей оси 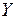 :
:
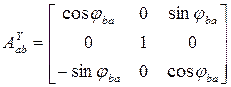
3) Поворот вокруг общей оси
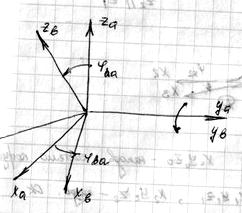
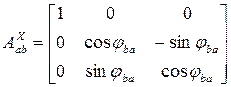
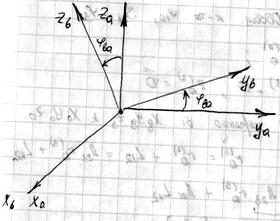
Составить преобразование из 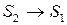
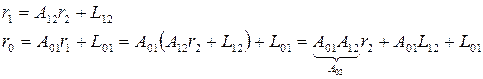
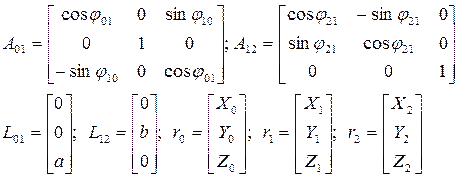
Прямая задача кинематики манипуляторов.
Задача состоит в определении положения, скоростей и ускорений его звеньев и отдельных точек по известным законам изменения его обобщенных координат.
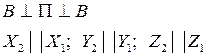
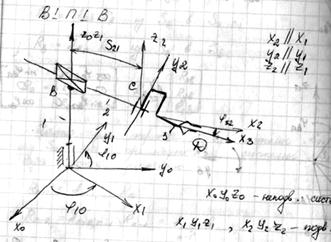
С каждым звеном связываем систему координат. 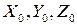 - неподвижная, остальные – подвижные.
- неподвижная, остальные – подвижные.
Обобщенные координаты:
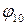 - угол поворота звена “1” относительно звена “0” вокруг оси
- угол поворота звена “1” относительно звена “0” вокруг оси 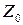
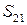 - перемещение звена “2” относительно звена “1” вдоль оси
- перемещение звена “2” относительно звена “1” вдоль оси 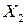
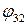 - угол поворота звена “3” относительно звена “2” вокруг оси
- угол поворота звена “3” относительно звена “2” вокруг оси 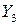
В задаче о положениях определим координаты центра схвата 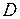 в неподвижной системе координат
в неподвижной системе координат 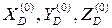 , если известны координаты точки
, если известны координаты точки 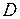 в системе
в системе 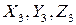
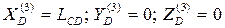
Для этого осуществляем последовательный переход от системы 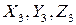 к системе
к системе 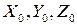
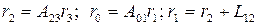
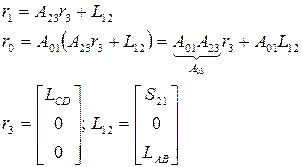
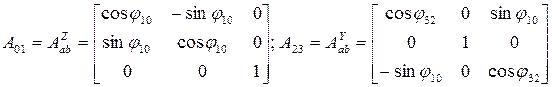
Матрица 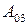 полностью определяет ориентацию руки “3” в неподвижной системе координат
полностью определяет ориентацию руки “3” в неподвижной системе координат 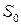 , так как столбцы этой матрицы представляют собой направление косинуса осей
, так как столбцы этой матрицы представляют собой направление косинуса осей 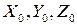
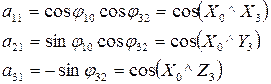
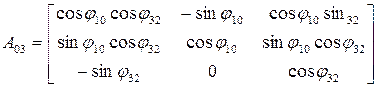
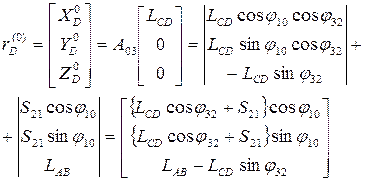
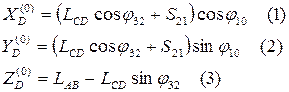
Угловая скорость любого звена манипулятора определяется на основании соотношения:
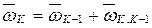
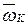 - абсолютная частота.
- абсолютная частота.
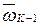 - переносная частота.
- переносная частота.
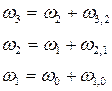
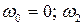 относительно звена “1”
относительно звена “1” 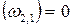 , так как звенья “2” и “1” связаны поступательной парой.
, так как звенья “2” и “1” связаны поступательной парой.
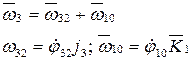
Запишем в неподвижной системе координат:
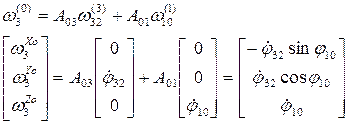
Угловое ускорение 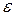 получим путем дифференцирования выражен
получим путем дифференцирования выражен
 2015-01-30
2015-01-30 2816
2816

 -
-