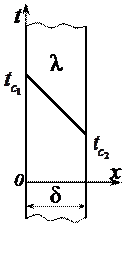 Постановка задачи. Имеется однородная изотропная стенка толщиной d с постоянным коэффициентом теплопроводности. Заданы граничные условия первого рода, т.е. температуры на внутренней и наружной поверхностях стенки: при
Постановка задачи. Имеется однородная изотропная стенка толщиной d с постоянным коэффициентом теплопроводности. Заданы граничные условия первого рода, т.е. температуры на внутренней и наружной поверхностях стенки: при 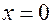
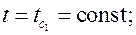 при
при 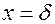
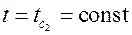 . По осям
. По осям 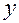 и
и 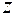 размеры стенки бесконечно большие (более чем на порядок превосходят размер стенки по оси
размеры стенки бесконечно большие (более чем на порядок превосходят размер стенки по оси 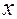 ). При таких условиях температура в стенке будет изменяться лишь в направлении оси х.
). При таких условиях температура в стенке будет изменяться лишь в направлении оси х.
Требуется найти закон распределения температуры по толщине стенки t = ¦(x) и получить выражения для определения плотности теплового потока (q) и теплового потока (Q).
Для нахождения закона распределения температуры по толщине стенки воспользуемся дифференциальным уравнением теплопроводности, с учетом того, что  (задача cтационарная),
(задача cтационарная), 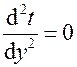 и
и 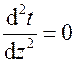 (температура по осям у и z не изменяется, так как размеры стенки по этим осям бесконечно большие). При этих условиях уравнение упрощается:
(температура по осям у и z не изменяется, так как размеры стенки по этим осям бесконечно большие). При этих условиях уравнение упрощается:
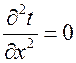 или
или 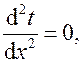
так как в этом случае частные и полные производные совпадают. Решая данное уравнения, получаем
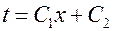 ,
,
где постоянные интегрирования находятся из граничных условий:
при 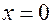
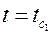 ; при
; при 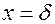
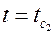 . Подставляя последовательно эти
. Подставляя последовательно эти
условия, находим постоянные интегрирования 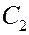 =
=  ,
, 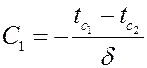 и получаем закон распределения температуры по толщине плоской стенки:
и получаем закон распределения температуры по толщине плоской стенки:
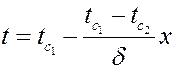 .
.
Выражение показывает, что температура по толщине стенки изменяется по линейному закону.
Плотность теплового потока определяется по закону Фурье. Градиент температуры 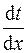 находится из уравнения:
находится из уравнения: 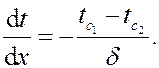 Подставляя это выражение в закон Фурье, получаем формулы для плотности теплового потока (
Подставляя это выражение в закон Фурье, получаем формулы для плотности теплового потока ( ) и теплового потока (
) и теплового потока (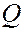 )
)
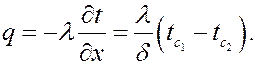
Q = q F =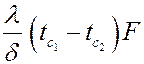 .
.
 2014-04-09
2014-04-09 1036
1036








