Ламинарное изотермическое течение несжимаемой жидкости в трубах

Предположим, что установившееся ламинарное движение жидкости происходит в горизонтальной, прямолинейной, круглой цилиндрической трубе с внутренним диаметром 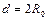, что соответствует одномерному течению. На некотором расстоянии от входа в нее, где поток уже сформировался (стабилизировался), выделим отрезок длиной l между сечениями 1-1 и 2-2.

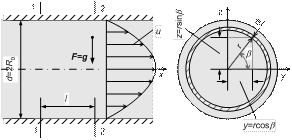
Рис. 1.3.

Пусть в сечении 1-1 давление равно p ₁, а в сечении 2-2 – p ₂ т.е. на длине l давление в потоке изменилось на величину 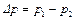за счет трения жидкости о стенки канала.

Применим к потоку жидкости уравнение Стокса (1.35), которое в рассматриваемом случае одномерного движения в проекции на ось x примет вид

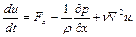
Выполним преобразование этого уравнения:

× исключим выражение, стоящее в левой части уравнения, поскольку в установившемся движении скорость не меняется с течением времени, следовательно ;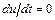

× удалим первое слагаемое в правой части уравнения, так как проекция силы тяжести на горизонтальную ось x равна нулю;

× в одномерном движении отсутствуют проекции вектора скорости на оси координат, перпендикулярные направлению движения, 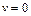и 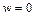. Поэтому и их производные равны нулю: 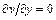и 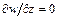. Следствием этого для несжимаемой жидкости будет

.

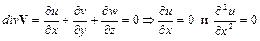На основании вышеизложенного проекция уравнения Стокса на ось x примет следующий вид

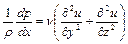. (1.36)

Изменение давления вдоль трубы пропорционально длине трубы

,

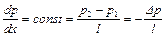поэтому уравнение (1.36) представим следующим равенством

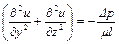. (1.37)

Решим полученное дифференциальное уравнение при условии, что на границе области течения (на стенке трубы) скорость частиц жидкости равна нулю

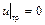. (1.38)

Граница области течения описывается уравнением окружности

.

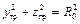Решением (1.37) является функция

. (1.39)

Она удовлетворяет граничному условию (1.38), а при 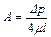превращает дифференциальное уравнение в тождество.

Это становится очевидным после подстановки (1.39) в уравнение (1.37)

.

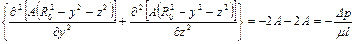Перейдем от декартовой системы координат к цилиндрической, в которой (см. рис. 1.3)

.

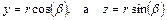Уравнение одномерного движения несжимаемой жидкости (1.39) в этой системе координат

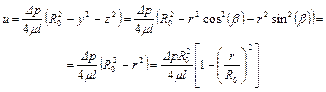
описывается квадратичной зависимостью скорости частицы жидкости от радиуса. Следовательно, при ламинарном течении профиль скорости, т.е. распределение векторов скорости по нормальному сечению потока, параболический.

Максимальная скорость имеет место в центре сечения трубопровода (при r= 0)

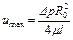. (1.40)

Применим полученный закон распределения скоростей для расчета объемного расхода жидкости. Элементарный расход через бесконечно малую площадку dS равен

.

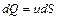Бесконечно малую площадку представим в виде кольца радиусом r и толщиной dr, т.е.

.

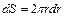Тогда после интегрирования по всей площади поперечного сечения, т.е. от r =0до r=R ₀, принимая во внимание независимость отношения 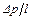от радиуса, получим

.

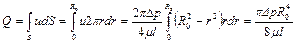Среднюю по сечению скорость находим делением расхода на площадь поперечного сечения канала

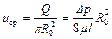. (1.41)

Ее значение в два раза меньше найденной ранее максимальной скорости на оси трубы.

Преобразовав полученное выражение, найдем закон сопротивления, т.е. зависимость потери давления на трение от расхода, либо средней скорости жидкости, ее вязкости и геометрических размеров канала

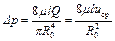. (1.42)

Из уравнения следует, что потери давления при ламинарном течении жидкости по прямолинейному каналу цилиндрической формы прямо пропорциональны его длине, расходу и вязкости среды в первой степени и обратно пропорциональны радиусу (диаметру) в четвертой степени. В литературе этот закон носит имя Пуазейля.

Выразив радиус трубы через диаметр, и выполнив ряд эквивалентных преобразований, данный закон можно представить в виде

,

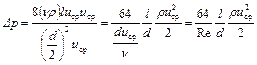где 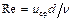– критерий Рейнольдса.

В технических расчетах принято потери давления на трение рассчитывать по формуле Дарси-Вейсбаха

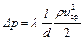, (1.43)

где l – коэффициент потерь на трение.

Из сравнения двух последних выражений следует, что при ламинарном режиме течения коэффициент потерь равен

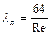. (1.44)

Изложенные результаты хорошо подтверждаются опытом, за исключением следующих случаев:

× при течении на начальном участке трубы, где еще происходит формирование потока;

× при течении с теплообменом;

× при течении в капиллярах и зазорах, где имеет место облитерация;

× при течении с большими перепадами давлений.