Уравнение движения тела переменной массы

Получим уравнение движения тела переменной массы (например, движение ракеты сопровождается уменьшением ее массы за счет истечения газов, образующихся от сгорания топлива).

Пусть в момент времени t масса ракеты m, а ее скорость 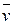; тогда по истечении времени dt ее масса уменьшится на dm и станет равной m–dm, а скорость увеличится до величины 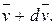Изменение импульса системы за время dt будет равно:

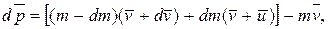
где 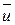- скорость истечения газов относительно ракеты. Раскрывая скобки в этом выражении, получим:

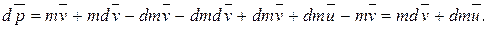
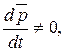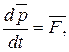Если на систему действуют внешние силы, то т.е. или 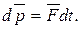Тогда 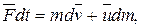или

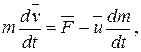(2.12)

где член 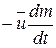называют реактивной силой 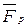. Если вектор 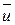противоположен 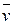, то ракета ускоряется, а если совпадает с 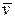, то тормозится.

Таким образом, уравнение движения тела переменной массы имеет следующий вид:

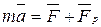(2.13)

Уравнение (2.13) называется уравнением И.В. Мещерского.

Применим уравнение (2.12) к движению ракеты, на которую не действуют никакие внешние силы. Тогда, полагая 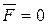и считая, что ракета движется прямолинейно (скорость истечения газов постоянна), получим:

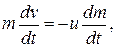
откуда

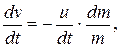
или

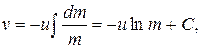
где С – постоянная интегрирования, определяемая из начальных условий. Если в начальный момент времени 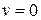, а стартовая масса ракеты составляет m₀, то 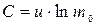.Следовательно,

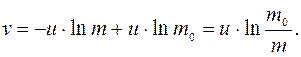(2.14)

Полученное соотношение называют формулой К.Э. Циолковского. Из выражения (2.14) следуют следующие практические выводы:

а) чем больше конечная масса ракеты m, тем больше должна быть стартовая масса m₀;

б) чем больше скорость истечения газов u, тем больше может быть конечная масса при данной стартовой массе ракеты.

Уравнения Мещерского и Циолковского справедливы для случаев, когда скорост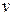и и 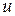намного меньше скорости света с.

Краткие выводы

· Динамика – раздел механики, предметом изучения которого являются законы движения тел и причины, которые вызывают или изменяют это движение.

· В основе динамики материальной точки и поступательного движения твердого тела лежат законы Ньютона. Первый закон Ньютона утверждает существование инерциальных систем отсчета и формулируется следующим образом: существуют такие системы отсчета, относительно которых поступательно движущиеся тела сохраняют свою скорость постоянной, если на них не действуют другие тела или действие других тел компенсируется.

· Инерциальной называется система отсчета, относительно которой свободная материальная точка, на которую не действуют другие тела, движется равномерно и прямолинейно, или по инерции. Система отсчета, движущаяся относительно инерциальной системы отсчета с ускорением, называется неинерциальной.

· Свойство любого тела оказывать сопротивление изменению его скорости называется инертностью. Мерой инертности тела при его поступательном движении является масса.

· Сила – это векторная физическая величина, являющаяся мерой механического воздействия на тело со стороны других тел или полей, в результате которого тело приобретает ускорение или изменяет свою форму и размеры.

· Второй закон Ньютона формулируется следующим образом: ускорение, приобретаемое телом (материальной точкой), пропорционально равнодействующей приложенных сил, совпадает с ней по направлению и обратно пропорционально массе тела:

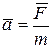, или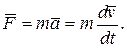

Более общая формулировка второго закона Ньютона гласит: скорость изменения импульса тела (материальной точки) равна равнодействующей приложенных сил:

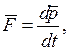
где 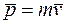- импульс тела. Второй закон Ньютона справедлив только в инерциальных системах отсчета.

· Всякое действие материальных точек (тел) друг на друга взаимно. Силы, с которыми действуют друг на друга материальные точки, равны по модулю, противоположно направлены и действуют вдоль соединяющей точки прямой (третий закон Ньютона):

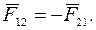
Эти силы приложены к разным точкам, действуют парами и являются силами одной природы.

· В замкнутой механической системе выполняется фундаментальный закон природы – закон сохранения импульса: импульс замкнутой системы материальных точек (тел) с течением времени не изменяется:

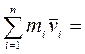const,

где n – число материальных точек в системе. Замкнутой (изолированной) называется механическая система, на которую не действуют внешние силы.

· Закон сохранения импульса является следствием однородности пространства: при параллельном переносе в пространстве замкнутой системы тел как целого ее физические свойства не изменяются.

Вопросы для самоконтроля и повторения

1. Какие системы отсчета называются инерциальными? Почему система отсчета, связанная с Землей, строго говоря, неинерциальна?

2. Какое свойство тела называется инертностью? Что является мерой инертности тела при его поступательном движении?

3. Что такое сила, чем она характеризуется?

4. Какие основные задачи решает ньютоновская динамика?

5. Сформулируйте законы Ньютона. Является ли первый закон Ньютона следствием второго закона?

6. В чем заключается принцип независимости действия сил?

7. Что называется механической системой? Какие системы являются замкнутыми (изолированными)?

8. Сформулируйте закон сохранения импульса. В каких системах он выполняется?

9. Каким свойством пространства обусловлена справедливость закона сохранения импульса?

10. Выведите уравнение движения тела переменной массы. Какие практические выводы позволяет сделать формула Циолковского?

Примеры решения задач

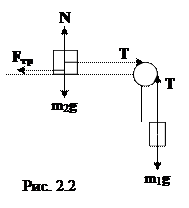
Задача 1. Грузы одинаковой массы (m₁=m₂ =0,5 кг) соединены нитью и перекинуты через невесомый блок, укрепленный на конце стола (рис. 2.2). Коэффициент трения груза m₂ о стол µ =0,15. Пренебрегая трением в блоке, определить: а) ускорение, с которым движутся грузы; б) силу натяжения нити.

Дано: m₁=m₂ =0,5 кг; µ =0,15.

Найти: а, Т.

 

Решение

По второму закону Ньютона уравнения

движения грузов имеют вид:

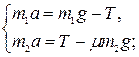
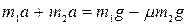, откуда

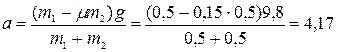м/с²;

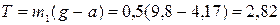Н.

Ответ: а =4,17 м/с², Т =2,82 Н.

Задача 2. Снаряд массой 5 кг, вылетевший из орудия, в верхней точке траектории имеет скорость 300 м/с. В этой точке он разорвался на два осколка, причем больший осколок массой 3 кг полетел в обратном направлении со скоростью 100 м/с. Определить скорость второго, меньшего, осколка.

Дано: m =5 кг; v =300 м/с; m₁ =3 кг; v₁ =100 м/с.

Найти: v₂.

Решение

По закону сохранения импульса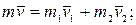

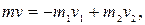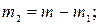
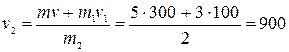где м/с.

Ответ: v₂ =900 м/с.

Задачи для самостоятельного решения

1. Тело массой 2 кг движется прямолинейно по закону 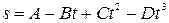, где С =2 м/с², D =0,4 м/с³. Определить силу, действующую на тело в конце первой секунды движения.

2. К нити подвешен груз массой 500 г. Определить силу натяжения нити, если нить с грузом: а) поднимать с ускорением 2 м/с²; б) опускать с тем же ускорением.

3. На тело массой 10 кг, лежащее на наклонной плоскости (угол α равен 20⁰), действует горизонтально направленная сила 8 Н. Пренебрегая трением, определить: а) ускорение тела; б) силу, с которой тело давит на плоскость.

4. С вершины клина, длина которого 2 м и высота 1 м, начинает скользить небольшое тело. Коэффициент трения между телом и клином μ=0,15. Определить: а) ускорение, с которым движется тело; б) время прохождения тела вдоль клина; в) скорость тела у основания клина.

5. Два груза с неравными массами m₁ и m₂ (m₁ > m₂) подвешены на легкой нити, перекинутой через неподвижный блок. Считая нить и блок невесомыми и пренебрегая трением в оси блока, определить: а) ускорение грузов; б) силу натяжения нити.

6. Платформа с песком общей массой М =2 т стоит на рельсах на горизонтальном участке пути. В песок попадает снаряд массой m =8 кг и застревает в нем. Пренебрегая трением, определить, с какой скоростью будет двигаться платформа, если в момент попадания скорость снаряда 450 м/с, а ее направление – сверху вниз под углом 30⁰ к горизонту.

7. На железнодорожной платформе, движущейся по инерции со скоростью 3 км/ч, укреплено орудие. Масса платформы с орудием 10 т. Ствол орудия направлен в сторону движения платформы. Снаряд массой 10 кг вылетает из ствола под углом 60⁰ к горизонту. Определить скорость снаряда (относительно Земли), если после выстрела скорость платформы уменьшилась в 2 раза.

8. Человек массой 70 кг находится на корме лодки, длина которой 5 м и масса 280 кг. Человек переходит на нос лодки. На какое расстояние лодка передвинется по воде относительно дна?

9. Шарик массой 200 г ударился о стенку со скоростью 10 м/с и отскочил от нее с такой же скоростью. Определить импульс, полученный стенкой, если до удара шарик двигался под углом 30⁰ к плоскости стенки.

10. Два шарика массами 2 и 4 кг двигаются со скоростями соответственно 5 и 7 м/с. Определить скорости шаров после прямого неупругого удара в случаях: а) больший шар догоняет меньший; б) шары двигаются навстречу друг другу.

ГЛАВА 3. РАБОТА И ЭНЕРГИЯ