В разделах 2.2., 2.3 рассматривались только квадратные матрицы. Здесь мы откажемся от этого требования. Пусть А – матрица размером m ´ n. Возьмем число k 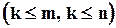 и отметим в матрице А какие–либо k строк и какие–либо k столбцов. Из элементов, стоящих на их пересечениях, составим определитель. Он называется минором k–го порядка матрицы А.
и отметим в матрице А какие–либо k строк и какие–либо k столбцов. Из элементов, стоящих на их пересечениях, составим определитель. Он называется минором k–го порядка матрицы А.
Пример 10.
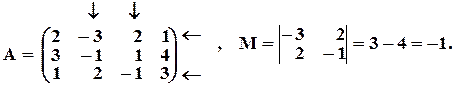
Здесь М минор 2–го порядка матрицы А. Конечно, миноров 2–го порядка в этой матрице много. Миноры 1–го порядка – это просто элементы матрицы, их в нашем примере 12. Миноров 3–го порядка – 4 штуки (строки нужно включать все, а из столбцов один не включать).
Если существует минор порядка r, не равный нулю, а все миноры больших порядков равны нулю, то число r называется рангом матрицы:
r = r(A) = rang(А).
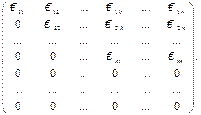 Пример 11. а)
Пример 11. а) 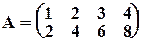 . Здесь r(A) = 1, так как легко заметить, что все миноры 2–го порядка равны 0.
. Здесь r(A) = 1, так как легко заметить, что все миноры 2–го порядка равны 0.
Рассмотрим сначала матрицы специального вида:
Если 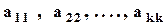 – не равные нулю числа, то такую матрицу будем называть матрицей трапецевидной формы. Последние нулевые строки могут и отсутствовать.
– не равные нулю числа, то такую матрицу будем называть матрицей трапецевидной формы. Последние нулевые строки могут и отсутствовать.
Пример 12. 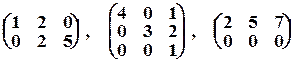 – матрицы трапецевидной формы. В последней из них k = 1 и форма трапеции не угадывается. Однако это – частный случай матрицы трапецевидной формы. Матрица
– матрицы трапецевидной формы. В последней из них k = 1 и форма трапеции не угадывается. Однако это – частный случай матрицы трапецевидной формы. Матрица 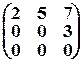 не имеет трапецевидной формы, так как в ней а22 = 0.
не имеет трапецевидной формы, так как в ней а22 = 0.
Теорема 3. Ранг матрицы трапецевидной формы равен числу её ненулевых строк.
Доказательство. Как и в примере 11, б), рассмотрим минор порядка k,
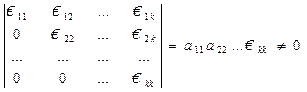
стоящий в левом верхнем углу:
.
В то же время любой минор большего порядка (если такой в этой матрице найдётся) равен нулю, так как содержит нулевую строку. Значит r(A) = k. Теорема доказана.
Теперь научимся приводить любую матрицу к трапецевидной форме, не меняя её ранга. Для этого используются так называемые элементарные преобразования:
1) перестановка строк;
2) прибавление к элементам строки соответствующих элементов другой строки, умноженных на одно и то же число;
3) перестановка столбцов;
4) преобразование столбцов, аналогичное указанному в пункте 2).
С этими преобразованиями мы уже встречались, изучая свойства определителей. Вспомним, что преобразования 2) и 4) не меняют величину определителя, а перестановки строк или столбцов могут лишь изменить знак. В частности, если определитель не равен нулю, то и после таких преобразований он не будет равен нулю. На основе этих рассуждений можно было бы и строго докaзать справедливость следующей теоремы.
Теорема 4. Элементарные преобразования неизменяютранг матрицы.
Теорема 5. Любую матрицу можно привести к трапецевидной форме, используя элементарные преобразования строк и перестановку столбцов.
Пример 13. Вычислить ранг матрицы 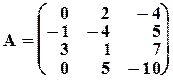 .
.


 Решение:
Решение: 
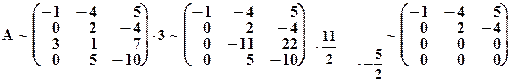
Получили трапецевидную матрицу с двумя ненулевыми строками. Значит, r(A) = 2.
 2015-01-30
2015-01-30 506
506








