Определитель – это число, которое по специальным правилам вычисляется для каждой квадратной матрицы. Определитель матрицы А будем обозначать так: | A |.
Иногда определитель обозначают символом detA и называют детерминантом, но мы будем пользоваться русским термином.
Определителем матрицы 2–го порядка называется число, которое записывается и вычисляется так:
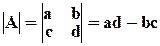 .
.
Пример 4. Пусть 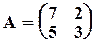 . Тогда
. Тогда 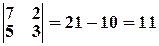 .
.
Определителем матрицы 3–го порядка называется число, которое записывается и вычисляется следующим образом:
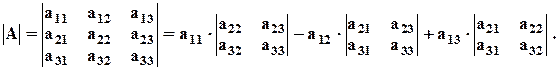
Рассмотрим внимательно эту формулу и сделаем такие наблюдения:
1) В формуле используются определители 2–го порядка, значит предполагается, что их мы вычислять уже умеем.
2) В формуле каждый элемент первой строчки умножается на определитель, который получится, если вычеркнуть строчку и столбик, где этот элемент стоит. Такой определитель будем называть минором соответствующего элемента aij и обозначать Mij. 
3)Перед произведением элемента а12 и минора М12 взят знак «-». Чтобы сформулировать и запомнить правило знаков, вводится понятие алгебраического дополнения. Алгебраическим дополнением элемента aij называется число
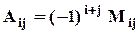 .
.
Другими словами, алгебраическое дополнение к элементу aij – это минор Mij, взятый со знаком «+ », если i + j – чётное число, или со знаком «-», если i + j – нечётное число.
Используя новые понятия, формулу для определителя 3–го порядка можно записать так:
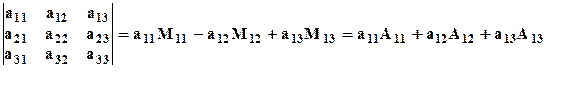 .
.
Перейдём теперь к общему случаю. Определителем квадратной матрицы порядка n называется число, которое записывается и вычисляется следующим образом:
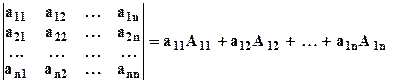 .
.
Эта формула называется разложением определителя по первой строке. Заметим, что в ней алгебраические дополнения вычисляются как определители порядка n-1. Такой подход использует принцип математической индукции: зная, как вычисляются определители 3–го порядка, можно вычислять определители 4–го порядка, и так далее: формула позволяет переходить к более высоким порядкам.
Рассмотрим свойства определителей.
Свойство 1. Определитель можно вычислить с помощью разложения по любой строке или по любому столбцу, т.е. определитель равен сумме произведений элементов любой строки (или столбца) на их алгебраические дополнения.
Свойство 2. При транспонировании матрицы величина ее определителя не меняется.
Доказательство. Проведем доказательство методом математической индукции по порядку определителя n.
База индукции. Для n = 2 свойство 2 легко проверяется:
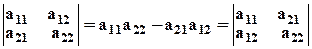 .
.
Свойство 3. Если в определителе поменять местами 2 строки, то он сменит знак.
Свойство 4. Сумма произведений элементов строки на алгебраические дополнения элементов другой строки равна нулю. т.е. при i ¹ j
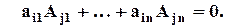
Свойство 5. Определитель не изменится, если к элементам какой–либо строки прибавить соответствующие элементы другой строки, умноженные на одно и то же число.
Свойство 6. Определитель произведения матриц равен произведению их определителей:| AB |=| A | × | B |.
Это свойство мы доказывать не будем, лишь поясним на примере.
Пример 9. Пусть 
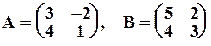 . Тогда
. Тогда
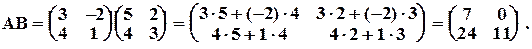
Вычислим определители:
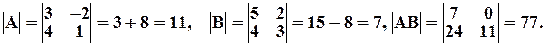
Итак, 
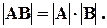
 2015-01-30
2015-01-30 1229
1229
