Матрицы

Курс лекций.

Матрицей называется прямоугольная таблица, состоящая из чисел. Например:

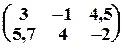В общем виде любую матрицу удобно записывать так:

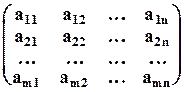Здесь a_ij – обозначение числа, стоящего на пересечении i –й строки и j –го столбика. Числа a_ij называются элементами матрицы. Особенно часто мы будем работать с квадратными матрицами, у которых m = n. Это число называется порядком квадратной матрицы. Можно рассматривать и матрицы, состоящие из одной строки (m = 1) или из одного столбца (n = 1).

Пример 1.

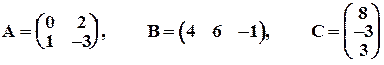Здесь А – квадратная матрица второго порядка (m = n = 2), В – матрица–строка, С –матрица–столбец. В матрице А: a₁₁ = 0, a₁₂ = 2, a₂₁ = 1, a₂₂ = – 3.

В матрице С: a₁₁ = 8, a₂₁ = – 3, a₃₁ = 3.

Матрицу любого размера, состоящую только из нулей, будем называть нулевой и обозначать буквой О:

О= .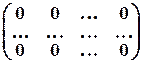

В квадратной матрице элементы 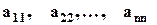составляют так называемую главную диагональ. Другая диагональ называется побочной.

побочная диагональ

главная диагональ

Квадратная матрица называется диагональной, если все элементы, не стоящие на главной диагонали, равны нулю. На главной диагонали могут быть любые числа. Если все они равны 1, то такая диагональная матрица называется единичной. Будем всегда обозначать ее буквой Е. Итак,

E = 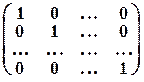– единичная, D = 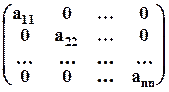– произвольная диагональная матрица.

Научимся выполнять простые действия с матрицами.

1) Умножение матрицы на число. Чтобы умножить матрицу на число нужно все ее элементы умножить на это число. Например:

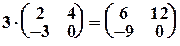2) Сложение матриц .. Складывать можно только матрицы одинакового размера. Сложение выполняется поэлементно:

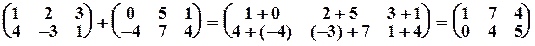. Правило сложения матриц в общем виде можно записать так: если

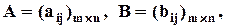то .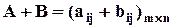

Здесь обозначение mxn указывает размерыматриц.

3) Умножение матриц.

Пусть 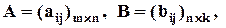т.е. число столбцов матрицы А равно числу строк матрицы В. Произведением AB называется матрица 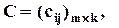элементы которой вычисляются по формуле:

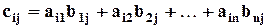Чтобы разобраться в этой формуле и запомнить её, возьмём i –ю строчку матрицы А и j– й столбик В (они должны быть равной длины). Перемножим первые элементы строчки и столбика, вторые элементы, и так далее. Затем все полученные произведения сложим:

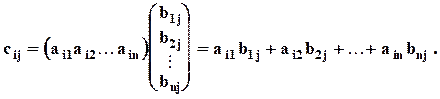
4) Транспонирование матриц.

Для любой матрицы А символом А^Т будем обозначать матрицу, у которой1–й, 2–й,... строками являются 1–й, 2–й,... столбцы матрицы А. Итак, если 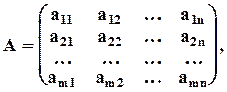то .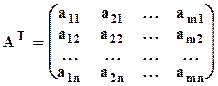

Для квадратной матрицы можно сказать, что транспонирование – это отражение относительно главной диагонали.

Пример 3.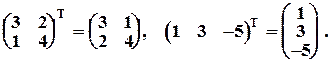

Теорема 1. Действия сложения и умножения матриц обладают следующими свойствами (для любых матриц А, В, С, с которыми эти действия можно выполнить):

(A + B) + C = A + (B + C) – ассоциативность сложения;

A + B = B + A – коммутативность сложения;