Геометрический смысл определенного интеграла

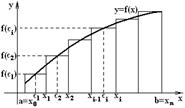
Определение. Фигура, ограниченная сверху графиком неотрицательной функции 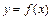, снизу осью 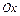, справа и слева – прямым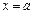и и 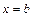, называется криволинейной трапецией.

Эта сумма будет приближенно равна площади криволинейной трапеции, 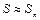. Если увеличить число разбиений, то при этом уменьшится длина частичного отрезка 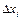, при этом 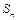будет более точно определять площадь трапеции. Поэтому за точное значение площади криволинейной трапеции принимают предел 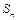при :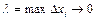

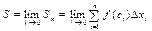, то есть .

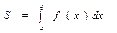Итак, определенный интеграл от неотрицательной функции численно равен площади криволинейной трапеции.