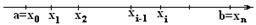 Пусть материальная точка
Пусть материальная точка 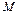 перемещается под действием силы
перемещается под действием силы 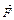 , направленной вдоль оси
, направленной вдоль оси 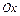 и имеющей переменную величину
и имеющей переменную величину 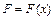 , где
, где 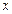 – абсцисса движущейся точки
– абсцисса движущейся точки 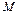 .
.
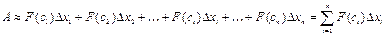 Разобьем отрезок
Разобьем отрезок  произвольным образом на
произвольным образом на 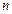 частичных отрезков длиной
частичных отрезков длиной 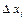 Так как длина частичного отрезка
Так как длина частичного отрезка 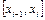 мала, то силу
мала, то силу 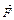 можно считать на данном отрезке постоянной и равной значению функции
можно считать на данном отрезке постоянной и равной значению функции 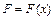 в произвольной точке
в произвольной точке 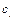 отрезка,
отрезка, 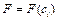 . Работа, совершенная этой силой на отрезке
. Работа, совершенная этой силой на отрезке 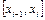 , равна
, равна 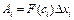 . Тогда работа
. Тогда работа  силы
силы  на всем отрезке
на всем отрезке  будет приближенно равна
будет приближенно равна
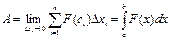 Данная сумма представляет собой интегральную сумму функции
Данная сумма представляет собой интегральную сумму функции 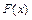 на отрезке
на отрезке  , а предел этой суммы при
, а предел этой суммы при 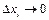 будет равен работе
будет равен работе 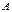 :
:
Физический смысл определенного интеграла состоит в том, что определенный интеграл численно равен работе силы 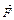 по перемещению точки
по перемещению точки 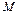 вдоль отрезка
вдоль отрезка  .
.
Формула Ньютона-Лейбница Пусть функция 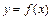 интегрируема на
интегрируема на  , непрерывна на отрезке
, непрерывна на отрезке  и
и 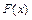 – какая-либо ее первообразная на
– какая-либо ее первообразная на  , то
, то 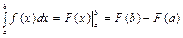 .
.
Пример. Вычислить интеграл 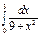 .Решение.
.Решение. 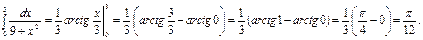
 2015-01-30
2015-01-30 1580
1580








