К данному методу интегрирования относятся интегралы вида:
1. 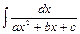 ; 2.
; 2. 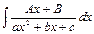 ; 3.
; 3. 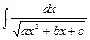 ; 4.
; 4. 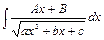 .
.
1. Рассмотрим интеграл 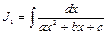 . Преобразуем квадратный трехчлен, выделив полный квадрат:
. Преобразуем квадратный трехчлен, выделив полный квадрат:
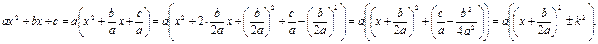 где
где 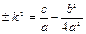 .
.
Таким образом, интеграл 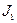 принимает вид:
принимает вид: 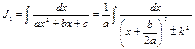 .Сделаем подстановку
.Сделаем подстановку 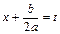 ,
, 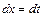 . Тогда получим
. Тогда получим 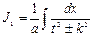 . Это уже табличные интегралы (в таблице 19 и 20).
. Это уже табличные интегралы (в таблице 19 и 20).
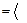
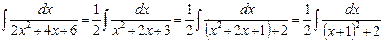 Пример. Найти интеграл
Пример. Найти интеграл 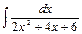 . Решение.
. Решение.
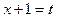 ,
, 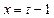 ,
, 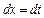
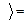
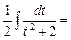
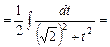
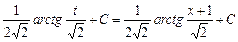 .
.
 Понятие определенного интеграла
Понятие определенного интеграла
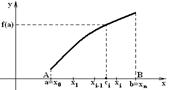
Пусть на отрезке  задана непрерывная функция
задана непрерывная функция 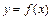 .Разобьем отрезок
.Разобьем отрезок  произвольным образом на
произвольным образом на 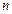 частей точками
частей точками 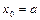 ,
, 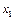 ,
, 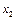 , …,
, …, 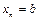 , причем
, причем 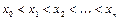 Длину частичного отрезка разбиения
Длину частичного отрезка разбиения 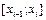 обозначим через
обозначим через 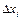 , то есть
, то есть 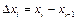 . В каждом частичном отрезке
. В каждом частичном отрезке 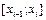 произвольным образом выберем точку
произвольным образом выберем точку 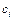 и найдем значение функции
и найдем значение функции 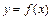 в каждой точке:
в каждой точке: 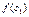 ,
, 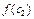 , …,
, …, 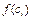 , …,
, …, 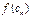 . Составим сумму
. Составим сумму
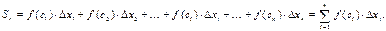
Данная сумма называется интегральной суммой для функции 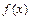 на отрезке
на отрезке  . Пусть
. Пусть 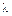 – длина наибольшего частичного отрезка:
– длина наибольшего частичного отрезка: 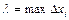 . Найдем предел интегральной суммы при
. Найдем предел интегральной суммы при 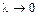 :
: 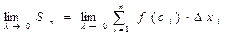 .
.
Определение 7. Если интегральная сумма 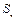 имеет предел
имеет предел 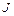 , который не зависит ни от способа разбиения отрезка
, который не зависит ни от способа разбиения отрезка  на частичные отрезки, ни от выбора точек
на частичные отрезки, ни от выбора точек 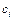 в них, то этот предел называют определенным интегралом от функции
в них, то этот предел называют определенным интегралом от функции 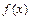 на отрезке
на отрезке  и обозначают
и обозначают 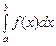 . Таким образом,
. Таким образом, 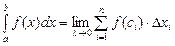 ,
,
где 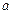 – нижний предел интегрирования,
– нижний предел интегрирования, 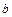 – верхний предел интегрирования,
– верхний предел интегрирования, 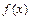 – подынтегральная функция,
– подынтегральная функция,
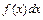 – подынтегральное выражение,
– подынтегральное выражение, 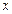 – переменная интегрирования,
– переменная интегрирования,  – отрезок интегрирования.
– отрезок интегрирования.
Теорема Коши. Если функция 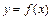 непрерывна на отрезке
непрерывна на отрезке  , то определенный интеграл
, то определенный интеграл 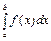 существует.
существует.
 2015-01-30
2015-01-30 674
674








