1. Определенный интеграл не зависит от обозначения переменной интегрирования: 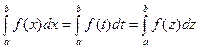 .
.
2. 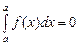 .
.
3. Постоянный множитель можно выносить за знак определенного интеграла: 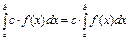 , где
, где 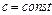 .
.
4. 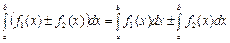 ,
, 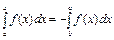 .
.
5. Если 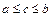 , то
, то 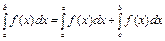 .
.
6. Теорема «о среднем». Если функция 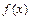 непрерывна на
непрерывна на  , точка
, точка 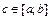 такая, что
такая, что 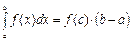 .
.
Число 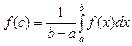 – среднее значение функции
– среднее значение функции 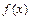 на отрезке
на отрезке  .
.
7. Если функция 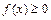 на отрезке
на отрезке  , то
, то 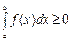 на этом отрезке.
на этом отрезке.
8. 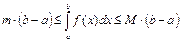 Если на отрезке
Если на отрезке 
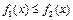 , то
, то 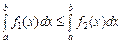 .
.
9. Если 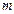 и
и 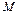 – соответственно наименьшее и наибольшее значения функции
– соответственно наименьшее и наибольшее значения функции 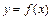 на отрезке
на отрезке  , то
, то
10. 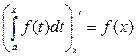
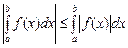 .
.
11. Производная определенного интеграла по переменному верхнему пределу равна подынтегральной функции
3.5 Замена переменной в определенном интеграле Пусть для вычисления интеграла 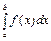 от непрерывной функции на отрезке
от непрерывной функции на отрезке  сделана подстановка
сделана подстановка 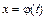 .
.
Теорема. Если:
1) функция 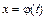 и ее производная
и ее производная 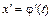 непрерывны на отрезке
непрерывны на отрезке 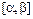 ,
,
2) 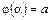 ,
, 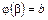 ,
,
3) функция 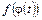 определена и непрерывна на отрезке
определена и непрерывна на отрезке 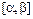 , то
, то 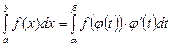 .
.
Пример. Вычислить интеграл 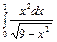 .
.
Решение. Сделаем тригонометрическую подстановку 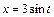 , тогда
, тогда 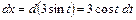 .
.
Найдем пределы интегрирования: если 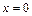 , то
, то 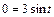 ,
, 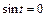 ,
, 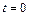 , если
, если 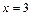 , то
, то 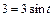 ,
, 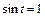 ,
, 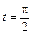 .
.
Тогда 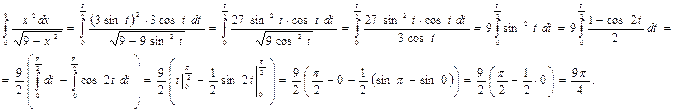
3.6 Интегрирование по частям Если функции 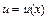 и
и 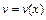 имеют непрерывные производные на отрезке
имеют непрерывные производные на отрезке  , то имеет место формула
, то имеет место формула 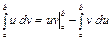 .
.
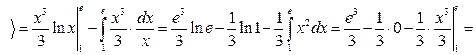 Пример. Вычислить интеграл
Пример. Вычислить интеграл 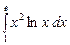
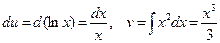
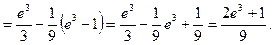 Решение.
Решение. 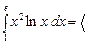 интегрирования по частям:
интегрирования по частям: 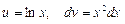 , тогда
, тогда
. Приложения определенного интеграла
 1. Вычисление площади плоской фигуры
1. Вычисление площади плоской фигуры
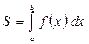 Из геометрического смысла определенного интеграла следует, что площадь криволинейной трапеции, ограниченной сверху кривой
Из геометрического смысла определенного интеграла следует, что площадь криволинейной трапеции, ограниченной сверху кривой 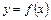 , снизу отрезком
, снизу отрезком 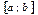 оси
оси 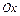 ,
,
 справа и слева прямыми
справа и слева прямыми 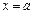 и
и 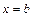 находится по формуле
находится по формуле
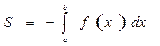 Если криволинейная трапеция расположена ниже оси
Если криволинейная трапеция расположена ниже оси 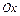 , то есть
, то есть 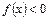 то площадь может быть найдена по формуле
то площадь может быть найдена по формуле
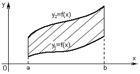
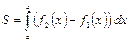 Площадь фигуры, ограниченной кривыми
Площадь фигуры, ограниченной кривыми 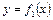 и
и 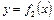 (
(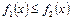 для любого
для любого 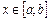 ), прямыми
), прямыми 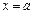 и
и 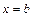 можно найти по формуле
можно найти по формуле
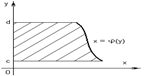
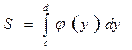 Если криволинейная трапеция ограничена справа непрерывной кривой
Если криволинейная трапеция ограничена справа непрерывной кривой 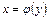 , слева отрезком
, слева отрезком 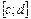 оси
оси 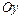 , снизу и сверху прямыми
, снизу и сверху прямыми 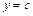 и
и 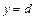 , то ее площадь находится по формуле
, то ее площадь находится по формуле
2. 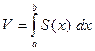
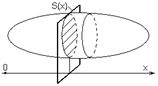 Вычисление объема тела по известным площадям параллельных сечений
Вычисление объема тела по известным площадям параллельных сечений
Если известны площади 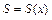 сечений тела плоскостями, перпендикулярными оси
сечений тела плоскостями, перпендикулярными оси 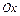 то объем данного тела находится по формуле
то объем данного тела находится по формуле
4. Пусть вокруг оси 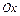 вращается криволинейная трапеция, ограниченная линией
вращается криволинейная трапеция, ограниченная линией 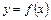 (
(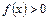 ), отрезком
), отрезком 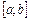 оси
оси 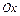 и прямыми
и прямыми 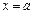 и
и 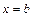 Полученная вращением фигура, называется телом вращения.
Полученная вращением фигура, называется телом вращения.
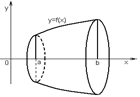 Объем тела вращения вокруг оси
Объем тела вращения вокруг оси 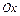
находится по формуле 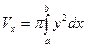 или
или 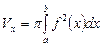 .
.
Если эту трапецию вращать вокруг оси 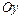 , то
, то 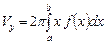 .
.
5. Вычисление работы переменной силы. Пусть материальная точка 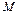 перемещается вдоль оси
перемещается вдоль оси 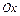 под действием переменной силы
под действием переменной силы 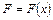 , направленной параллельно этой оси. Работа, произведенная силой при перемещении точки
, направленной параллельно этой оси. Работа, произведенная силой при перемещении точки 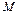 из положения
из положения 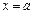 в положение
в положение  , находится по формуле
, находится по формуле 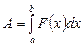 .
.
6. Путь, пройденный телом Пусть материальная точка 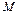 перемещается по прямой с переменной скоростью
перемещается по прямой с переменной скоростью 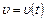 . Тогда путь
. Тогда путь 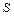 , пройденный данной точкой за промежуток времени от
, пройденный данной точкой за промежуток времени от 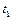 до
до 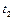 , может быть вычислен по формуле
, может быть вычислен по формуле 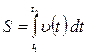 .
.
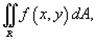 Определение двойного интеграла
Определение двойного интеграла
Понятие интеграла может быть расширено на функции двух и большего числа переменных. Рассмотрим, например, функцию двух переменных z = f (x,y). Двойной интеграл от функции f (x,y) обозначается как
 где R - область интегрирования в плоскости Oxy. Если определенный интеграл
где R - область интегрирования в плоскости Oxy. Если определенный интеграл
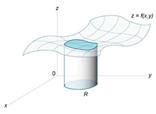
 от функции одной переменной выражает площадь под кривой f (x) в интервале от x = a до x = b, то двойной интеграл выражает объем под поверхностью z = f (x,y) выше плоскости Oxy в области интегрирования R (рисунок 1).
от функции одной переменной выражает площадь под кривой f (x) в интервале от x = a до x = b, то двойной интеграл выражает объем под поверхностью z = f (x,y) выше плоскости Oxy в области интегрирования R (рисунок 1).
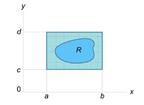
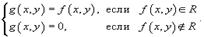 Чтобы определить двойной интеграл в произвольной области R, отличной от прямоугольной, выберем прямоугольник
Чтобы определить двойной интеграл в произвольной области R, отличной от прямоугольной, выберем прямоугольник 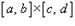 , покрывающий область R (рисунок 3), и введем функцию g (x,y), такую, что
, покрывающий область R (рисунок 3), и введем функцию g (x,y), такую, что
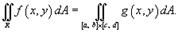 Тогда двойной интеграл от функции f (x,y) в произвольной области R определяется как
Тогда двойной интеграл от функции f (x,y) в произвольной области R определяется как
Свойства двойного интеграла Двойной интеграл обладает следующими свойствами:
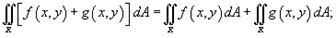
1)
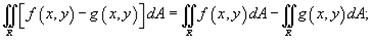 2)
2)
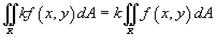 3), где k - константа;
3), где k - константа;
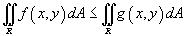
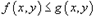
4) Если в области R, то;
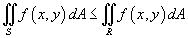
5) Если 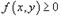 в области R и (рисунок 4), то; Рис.4
в области R и (рисунок 4), то; Рис.4
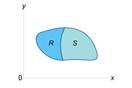
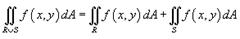
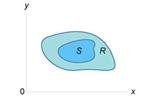
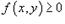 6) Если на R и области R и S являются непересекающимися (рисунок 5), то.
6) Если на R и области R и S являются непересекающимися (рисунок 5), то.
Рис.5
Здесь 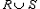 означает объединение этих двух областей.
означает объединение этих двух областей.
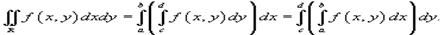 Двойные интегралы в прямоугольной области. Пусть область интегрирования R представляет собой прямоугольник
Двойные интегралы в прямоугольной области. Пусть область интегрирования R представляет собой прямоугольник 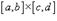 . Тогда двойной интеграл в такой области выражается через повторный интеграл в следующем виде:
. Тогда двойной интеграл в такой области выражается через повторный интеграл в следующем виде:
Обычно удобнее начинать интегрировать функцию f (x,y). с более простого интеграла. В частном случае, когда подынтегральная функция f (x,y) "расщепляется" на произведение f (x)g(y), двойной интеграл равен произведению двух определенных интегралов: 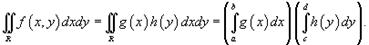
Пример 1 Вычислить двойной интеграл 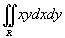 в области
в области 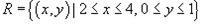 .
.
Решение. Как видно, подынтегральная функция f (x,y) представляет собой произведение f (x)g(y). Следовательно, интеграл равен
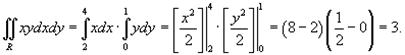
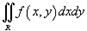 Геометрические приложения двойных интегралов
Геометрические приложения двойных интегралов
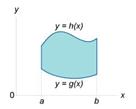 1. Площадь плоской фигуры. Если f (x,y) = 1 в интеграле, то двойной интеграл равен площади области интегрирования R.
1. Площадь плоской фигуры. Если f (x,y) = 1 в интеграле, то двойной интеграл равен площади области интегрирования R.
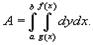 Площадь области типа I (элементарной относительно оси Оy) (рисунок 1) выражается через повторный интеграл в виде
Площадь области типа I (элементарной относительно оси Оy) (рисунок 1) выражается через повторный интеграл в виде
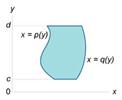
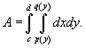 Аналогично, площадь области типа II (элементарной относительно оси Оx) (рисунок 2) описывается формулой
Аналогично, площадь области типа II (элементарной относительно оси Оx) (рисунок 2) описывается формулой
 2015-01-30
2015-01-30 1087
1087