Сплошной и выборочный контроль

Сплошной контроль приборов при производстве требует больших за­трат и осуществляется для дорогостоящих изделий, когда отказ даже одной детали приводит к катастрофическим последствиям. Однако в некоторых отраслях, например, в производстве бытовых приборов, в автомобилестроении, при использовании 100% контроля было бы невозможно по экономическим соображениям продавать продукцию покупателям со средними доходами. Альтернативами 100% контроля являются:

· отладка техпроцесса и обеспечение стабильности необходимого уровня качества;

· выборочный контроль.

Выборочный контроль выгоден, когда:

· сплошной контроль не возможен (например, при разрушающем контроле или когда на его осуществление требуется много времени);

· в случаях, когда поштучный контроль не имеет смысла (например, при штамповке, литье пластмасс и т.п.);

· в случаях, когда выборочный контроль выгоден в экономическом отношении.

Зависимость стоимость контроля качества от фактического уровня качества при различных методах контроля можно проиллюстрировать с помощью следующего рисунка.

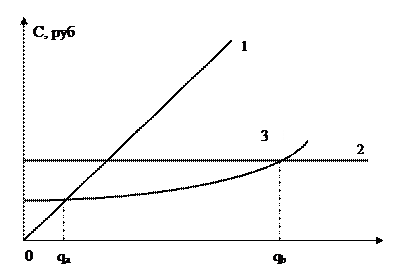
Рис.6.1. Зависимость стоимости контроля от уровня качества.

Прямая 1 показывает динамику затрат при отсутствии контроля. Очевидно, что убытки в этом случае прямо пропорциональны доле брака в продукции. При сплошном контроле (прямая 2) затраты на контроль не завися от доли брака. При выборочном (его еще иногда называют статистическим) контроле (3) затраты складываются из непосредственных затрат на контроль и на компенсацию убытков от пропущенного брака.

При этом:

· если доля брака q < q_a, то осуществлять контроль не целесообразно;

· при доле брака q_a < q < q_b наиболее экономически эффективен выборочный контроль;

· если q > q_b необходимо использовать сплошной контроль.

Пример 6.1. Известно, что С – стоимость контроля детали 0,2 руб, а доля дефектных деталей р – 0,05 (необходимо проконтролировать в среднем 1/р т.е. 20 деталей чтобы выявить одну дефектную). Тогда затраты на выявление 1 дефектной детали 0,2´20 = 4 руб. Если стоимость одной детали к = 2 рубля, то р = с\к представляет собой допустимый уровень брака сверх которого разбраковка продукции, сплошной контроль, является экономичной (в нашем случае р = 0,1).

В процессе выборочного контроля решают следующие задачи:

1) проверка, настроенности и устойчивости технологического процес­са;

2) определение минимального объема выборки;

3) проверка достоверности контроля;

4) сравнение однородных средних или дисперсий для оценки, например, идентичности 2-х техпроцессов.

Вероятный брак изделий (систематические и случайные погрешности) как и погрешности при производстве носят случайный характер, поэтому решение упомянутых задал базируется на теории вероятностей и математи­ческой статистике.

Построение плана выборочного контроля. Возможны два способа про­ведения выборочного контроля качества продукции. Различают контроль:

· по количественному признаку – по уровню параметра (например, по ТУ размер должен быть 7_{- 0,15}, а контроль показывает 7,01). Качество партии определяется на основании статистического анализа распределения выходных параметров изделий, прошедших испытания;

· по качественному признаку, (по доле брака) когда измерительный прибор разделяет продукцию по определенным категориям (например, детали с размером выше номинального, или ниже номинального).

Рассмотрим более подробно второй способ, имеющий широкое применение при контроле качества продукции, например, при массовом производстве дешевых бытовых приборов.

При производстве контроль качества больших партий продукции осу­ществляется с помощью контроля показателей качества случайной выборки. Если уровень качества изделий в выборке соответствует установленным требованиям, то считают, что всю партию можно принять как годную. В противном случае партия бракуется.

В ряде случаев вся партия может быть ошибочно забракована, и это считается ошибкой первого рода, или риском поставщика. Ошибка противоположного свойства называется ошибкой второго рода или риском заказчика. Обе ошибки выражаются в процентах и оговариваются в технической документации.

Если долю дефектных изделий в партии обозначить как q, то

q = N_D /N, (6.1)

где N и N_D - соответственно число дефектных деталей и их общее число.

q_n = Z / n, (6.2)

где q_n - доля дефектных деталей в выборке;

Z - число бракованных деталей;

n - объем выборки.

В случае, если бы генеральная совокупность и выборка имели распределение деталей по закону равной вероятности, то выборочный контроль значительно бы упростился. На практике q ≠ q_n что и является причиной ошибок обоих родов при выборочном контроле. Если q < q_n, то возникает ошибка первого рода и наоборот.

В разных условиях получают разные законы распределения вероятностей попадания годных и дефектных изделий в выборку, поэтому следует правильно выбирать математический аппарат для оценки качества контроля.

При выборочном контроле имеют место в основном биноминальный, гипергеометрический, Пуассона и нормальный закон распределения. Первые три являются законами распределения случайных величин и используются при контроле по качественному признаку, когда каждое отдельно испытание в серии имеет только два исхода: изделие годное или дефектное. Нормальный закон используется при кон­троле по количественным признакам [24].

Биноминальное распределение.

Вероятность Р(n,z) появления в выборке объемом n числа z де­фектных изделий определяется по формуле:

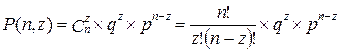, (6.3)

где q — вероятность появления брака;

р — вероятность появления годного изделия;

С^z_n — сочетание из n элементов по z;

q и р — характеризуют устойчивость технологического процесса.

Допустим, что n = 30; q = 0,05; р = 0,95.

Р(n,z) = P(30,z) — решение существует только в табличном виде и нужно задавать z в виде таблицы от 0 до z.

Пример 6.2. Вычислить в выборке число z дефектных изделий, где 0 £ z < 9; q = 0,05; р = 0,95; n = 30.