2015-01-30
281
По заданному логическому выражению:
- составить исходную структурную схему
- составить исходную таблицу истинности
- используя логические тождества упростить логическое выражение (аналитическая минимизация).
- для полученного выражения составить структурную схему
- составить новую таблицу истинности
- если новая и исходная таблица истинности совпадает – всё нормально, если нет – проверить расчёты
Проделать минимизацию для двух наборов элементов:
1.И, ИЛИ, НЕ;
2.И–Не, ИЛИ–НЕ.
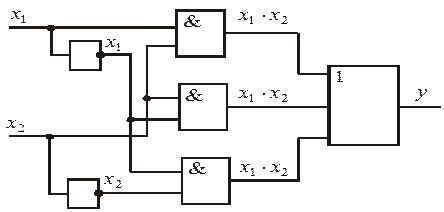
Пример минимизации.
Составим логическое выражение для этой функции.
Таблица истинности.
| X1 | X2 |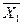 
| 
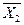
| X1·X2 |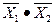 
| 
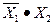
| Y=A+B+C |
Проведём минимизацию для набора элементов и – не, или – не.
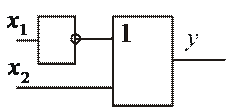Как правило это осуществляется использованием правила де Моргана для получения результата (все элементы должны иметь операцию инверсии на выходе – обозначается кружком на выходе схемы), либо возвращением обратно по преобразованиям до операции инверсии.
| X1 | X2 |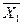
| 
|
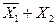
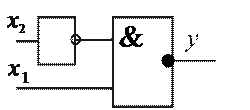
| X1 | X2 |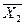 
| 
|
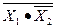
Продолжение триггеров.
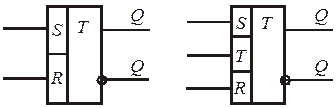
Имеются также другие типы триггеров.
Наиболее распространённые:
Т – триггер (тактируемый).
D – триггер (синхронизируемый).
JK – триггер
Т – триггер
 |
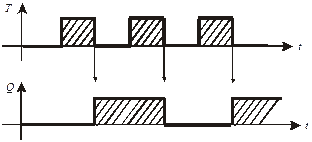Входы R и S работают также как и у R – S триггеров.
