Выберем в пространстве 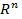 некоторый базис
некоторый базис 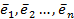 . Пусть
. Пусть 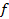 - линейное преобразование
- линейное преобразование 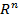 . Рассмотрим вектор
. Рассмотрим вектор 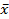 и его образ
и его образ 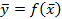 . Разложим эти векторы по базису
. Разложим эти векторы по базису
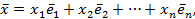 (4.1)
(4.1)
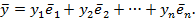 (4.2)
(4.2)
В виду линейности отображения f следует
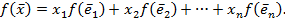 (4.3)
(4.3)
Векторы 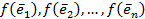 также допускают разложение по базису
также допускают разложение по базису
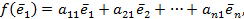
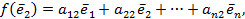
……………………………………
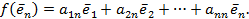
Если подставить эти выражения в равенство (4.3), то получим
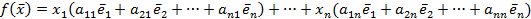
или
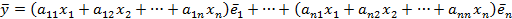
Сравнивая это представление вектора 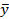 с (4.2), приходим к искомым формулам:
с (4.2), приходим к искомым формулам:
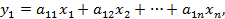
……………………………………
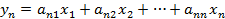 .
.
Формулы можно записать в виде матричного уравнения
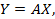
где
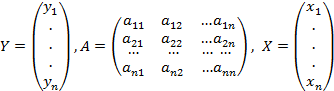 .
.
Матрица А называется матрицей линейного преобразования f в данном базисе 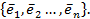
 2014-10-30
2014-10-30 670
670








