Тема 5. Квадратичные формы

Определение. Квадратичной формой 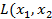,…, 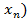от п переменных называется сумма, каждый член которой является либо квадратом одной из этих переменных, либо произведением двух разных переменных, взятых с некоторым коэффициентом:

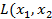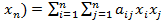,…, . (5.1)

Коэффициенты 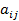– действительные числа, причём 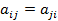. Матрица А = (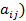, составленная из этих коэффициентов, называется матрицей квадратичной формы.

В матричной записи квадратичная форма имеет вид

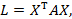
где Х – вектор-столбец переменных.

То есть

,…,

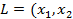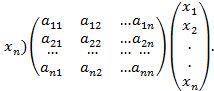
Пример. Дана квадратичная форма 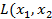, 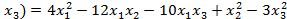. Записать её в матричном виде.

Решение. На диагонали лежат коэффициенты при квадратах переменных, а другие элементы – половинам соответствующих коэффициентам квадратичной формы. Следовательно,

,

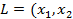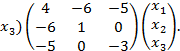
Выясним, как изменяется квадратичная форма при невырожденном линейном преобразовании переменных.

Пусть вектор-столбцы переменных X и Y связаны линейным соотношением 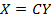, где 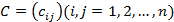есть некоторая невырожденная матрица п -го порядка. Тогда квадратичная форма

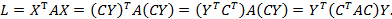
Итак, при невырожденном линейном преобразовании 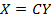матрица квадратичной формы имеет вид

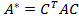(5.2)

Формулы 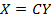можно истолковывать как формулы преобразования координат вектора при переходе к новому базису, поэтому равенство (5.2) можно рассматривать ка выражение для матрицы квадратичной формы L в новом базисе.

Пример. Дана квадратичная форма 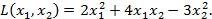Найти квадратичную форму 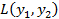, полученную из данной, линейным преобразованием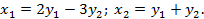

Решение. Матрица квадратичной формы 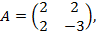а матрица линейного преобразования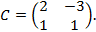

Следовательно, по формуле (5.2) матрица искомой квадратичной формы

,

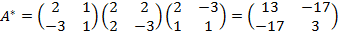а квадратичная форма имеет вид .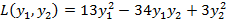

Определение. Каноническим видом квадратичной формы называется выражение

.

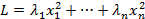Особенность этого вида в том, что отсутствуют члены с произведением различных координат.

Определение. Нормальным видом квадратичной формы называется выражение

.

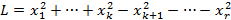Этот вид характеризуется тем, что входящие в него квадраты переменных имеют коэффициенты плюс или минус единица. Количество слагаемых в этой формуле равно рангу 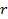квадратичной формы.