Определение. Ненулевой вектор 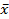 линейного пространства V называется собственным вектором линейного преобразования f, если выполняется равенство
линейного пространства V называется собственным вектором линейного преобразования f, если выполняется равенство
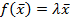 , (4.4)
, (4.4)
где 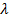 – некоторое число. При этом число
– некоторое число. При этом число 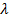 называется с обственным значением линейного преобразования f. Говорят также, что
называется с обственным значением линейного преобразования f. Говорят также, что 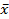 есть собственный вектор,принадлежащийсобственному значению
есть собственный вектор,принадлежащийсобственному значению 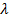 .
.
Пусть А – матрица линейного преобразования f в базисе 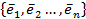 и Х - матрица-столбец из координат вектора
и Х - матрица-столбец из координат вектора 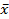 , тогда соотношение (5.4) может быть записано в матричной форме
, тогда соотношение (5.4) может быть записано в матричной форме
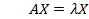 . (4.5)
. (4.5)
Принято говорить, что ненулевая матрица-столбец Х является собственным вектором квадратной матрицы А, соответствующим собственному значению 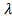 .
.
Уравнение (4.5) может быть переписано в виде
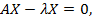
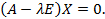
Однородная система уравнений тогда и только тогда имеет ненулевое решение, когда её определитель равен нулю, т.е.
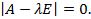 (4.6)
(4.6)
Определение. Уравнение (4.6) называется характеристическим уравнением матрицы А.
Таким образом, собственные значения матрицы А являются корнями её характеристического уравнения.
Предложение. Собственные значения матриц А и АТ совпадают.
Пример. Найти собственные значения и собственные векторы матрицы
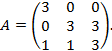
Решение. Запишем характеристическое уравнение
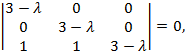
или 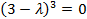 . Следовательно,
. Следовательно, 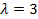 – единственное собственное значение матрицы А. Система уравнений для отыскания собственных векторов сводится к единственному уравнению
– единственное собственное значение матрицы А. Система уравнений для отыскания собственных векторов сводится к единственному уравнению
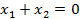 ,
,
или 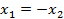 . Положим
. Положим 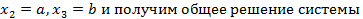
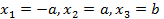 , то ест собственный вектор
, то ест собственный вектор 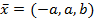 представляется в виде линейной комбинации
представляется в виде линейной комбинации
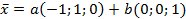
двух линейно независимых векторов 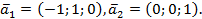
Замечание. Одному собственному значению может соответствовать несколько линейно независимых собственных векторов.
Пример. Найти собственные векторы и собственные значения матрицы
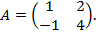
Решение. Запишем характеристическое уравнение
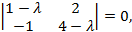
или 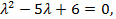 откуда
откуда 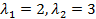 . Найдём собственные векторы. Подставим
. Найдём собственные векторы. Подставим 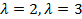 в систему уравнений
в систему уравнений 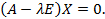
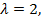
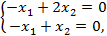
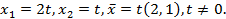
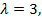
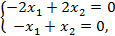
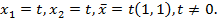
 2014-10-30
2014-10-30 850
850








